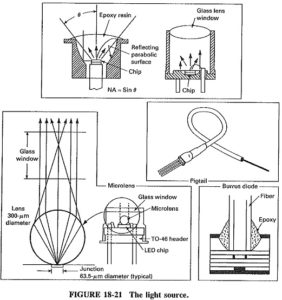
Digital Fundamentals:
The meaning of the term “digital” is fundamental to an understanding of the benefits of digital technology. Digital Fundamentals data must be compared with analog data in order to understand the distinction between the two. An analog signal is best illustrated by a sine wave as shown in Figure 14-1. Notice that the sine wave is continuous, and the value of the analog signal at any given instant can be anywhere within the range of the signal’s extremes.
The digital signal does not provide this continuous representation of the original signal. Instead, the digital signal represents data as a series of digits such as a number. This Digital Fundamentals representation can be considered as a code which approximates the actual value. Various digital systems are available.
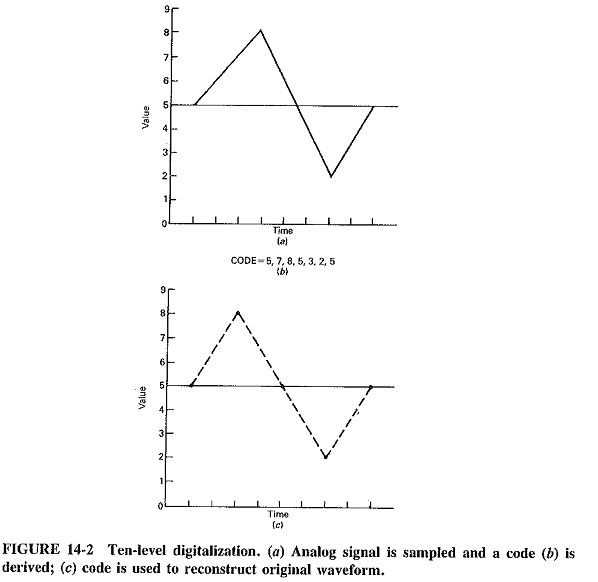
For example, a digital system which is decimal in nature can be used to represent the sine wave. To do this, the range of values would be divided into 10 levels. The signal would then be sampled at set intervals and the appropriate level at that instant would be determined. Since only 10 levels would be available, however, the level which is closest would be used for a given sample if the signal were not to fall exactly on one of the levels. As shown in Figure 14-2, the code could later be used to reconstruct the signal, producing a waveform similar to the original, with only minor discrepancies.
The Binary System:
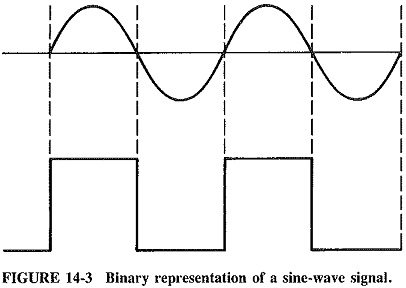
The binary system is based on the binary numbering system. This system has only two numbers, 0 and 1. If the sine wave is represented by the most basic binary system, a 1 will be generated if the signal value is above the halfway point. A 0 will result from signals below the halfway point. Figure 14.3 shows the binary representation of the sine-wave signal. A series of the sine-wave cycles would generate a series of pulses with spaces between them as shown.
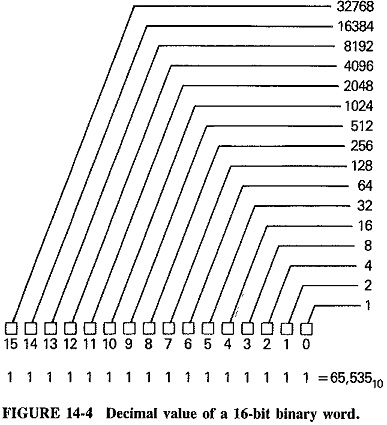
The word “digital,” as it is commonly used in information systems, refers to information coded in the form of binary states. A binary code consists of a series of binary digits (or “bits”) each of which can have either of only two values, either a 1 or a 0. When bits are assembled together into a group of a particular length (4 bits), they form a binary word, sometimes called a byte. A single binary character can represent only two pieces of information, 0 or 1. As bits are assembled into words several bits in length, however, the number of code combinations increases. A binary word 2 bits in length can have four different forms, 00, 01, 10 and 11, while a 3-bit word can have eight code combinations. The number of possible combinations increases by powers of 2, so that binary words 8 bits in length have 256 different forms and 16-bit binary words provide over 65,000 code combinations. Figure 14-4 illustrates the decimal value of the bits in a 16-bit binary word.
If information is reduced to a standard set of codes which can be represented by binary words, the information can be handled by Digital Fundamentals electronic devices. This is what is done in computers and digital processing systems. Digital computer codes are often based on the binary number system.