Smith Chart for Transmission Line:
The various properties of transmission lines may be represented graphically on any of a large number of charts. The most useful representations are those that give the impedance relations along a lossless line for different load conditions. The most widely used calculator of this type is the Smith Chart for Transmission Line.
Fundamentals of the Smith Chart:
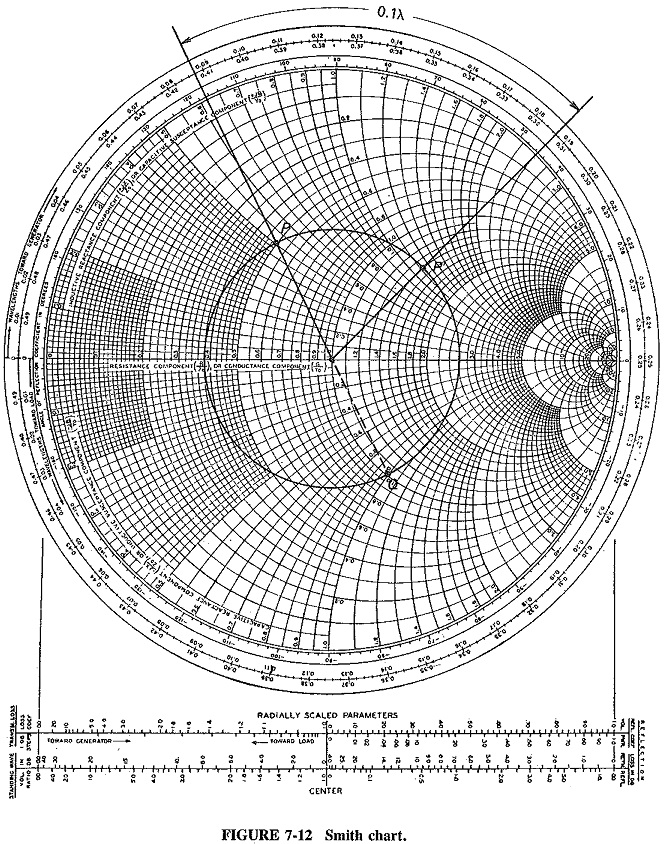
Description The polar impedance diagram, or Smith Chart for Transmission Line as it is more commonly known,, is illustrated in Figure 7-12. It consists of two sets of circles, or arcs of circles, which are so arranged that various important quantities connected with mismatched transmission lines may be plotted and evaluated fairly easily. The complete circles, whose centers lie on the only straight line on the chart, correspond to various values of normalized resistance (r = R/Z0) along the line. The arcs of circles, to either side of the straight line, similarly correspond to various values of normalized line reactance jx = jX/Z0. A careful look at the way in Which the circles intersect shows them to be orthogonal. This means that tangents drawn to the circles at the point of intersection would be mutually perpendicular. The various circles and coordinates have been chosen so that conditions on a line with a given load (i.e., constant SWR) correspond to a circle drawn on the chart with its center at the center of the chart. This applies only to lossless lines. In the quite rare case of lossy RF lines, an inward spiral must be drawn instead of the circle, with the aid of the scales shown in Figure 7-12 below the chart.
If a load is purely resistive, R/Z0 not only represents its normalized resistance but also corresponds to the standing-wave ratio, as shown in Equation (7-8). Thus, when a particular circle has been drawn on a Smith chart, the SWR corresponding to it may be read off the chart at the point at which the drawn circle intersects the only straight line on the chart, on the right of the chart center. This SWR is thus equal to the value of r ± j0 at that point; the intersection to the left of the chart center corresponds to 1/r. It would be of use only if it had been decided always to use values of SWR less than 1.
The greatest advantage of the Smith Chart for Transmission Line is that travel along a lossless line corresponds to movement along a correctly drawn constant SWR circle. Close examination of the chart axes shows the chart has been drawn for use with normalized impedance and admittance. This avoids the need to have Smith charts for every imaginable value of line characteristic impedance. (If a particular value of Z0 is employed widely or exclusively, it becomes worthwhile to construct a chart for that, particular value of Z0. For example, the General Radio Company makes a 50-Ω chart for use with its transmission equipment. It may also be used for any other 50-Ω situations and avoids the need for normalization.) Also note that the chart covers a distance of only a half-wavelength, since conditions repeat exactly every half-wavelength on a lossless line. The impedance at 17.716 λ away from a load on a line is exactly the same as the impedance 0.216 λ from that load and can be read from the chart.
Bearing these two points in mind, we see that impedance encountered at successive points along a lossless line may easily be found from the chart. They lie at corresponding successive points along the correct drawn (this word is repeated to emphasize the fact that such a circle must be drawn by the user of the chart for each problem, as opposed to the numerous circles already present on the Smith chart) constant SWR circle on the chart. Distance along a line is represented by (angular) distance around the chart and may be read from the circumference of the chart as a fraction of a wavelength. Consider a point some distance away from some load. If to determine the line impedance at 0.079 λ away from this new point, it quickly becomes evident that there are two points at this distance, one closer to the load and one farther away from it. The impedance at these two points will not be the same. This is evident if one of these points just happens to be a voltage node. The other point, being 2 x 0.079 = 0.158 λ away from the first, cannot possibly be another voltage node. The same reasoning applies in all other situations. The direction of movement around a constant SWR circle is also of importance. The Smith Chart for Transmission Line has been standardized so that movement away from the load, i.e., toward the generator, corresponds to clockwise motion on the chart. Movement toward the load corresponds to counterclockwise motion; this is always marked on the rim of commercial Smith Chart for Transmission Line and is shown in Figure 7-12.
For any given load, a correct constant SWR circle may be drawn by normalizing the load impedance, plotting it on the chart and then drawing a circle through this point, centered at 0. The point P in Figure 7-12 represents a correctly plotted normalized impedance of z = 0.5 + j0.5. Since it lies on the drawn circle which intersects the r axis at 2.6, it corresponds to an SWR of 2.6. If the line characteristic impedance had been 300 Ω, and if the load impedance had been (150 + j150) Ω, then P would correctly represent the load on the chart, and the resulting line SWR would indeed be 2.6. The impedance at any other point on this line may be found as described, by the appropriate movement from the load around the SWR = 2.6 circle. As shown in Figure 7-12, the normalized impedance at P′ is 1.4 + j1.1, where P′ is 0.100 λ away from the load.
The following are some of the more important applications of the Smith chart:
1. Admittance calculations. This application is based on the fact that the impedance measured at Q is equal to the admittance at P, if P and Q are λ/4 apart and lie on the same SWR circle. This is shown in Figure 7-12. The impedance at Q is 1 – j1, and a very simple calculation shows that if the impedance is 0.5 + j0.5, as it was at P, then the corresponding admittance is indeed 1 – j1, as read off at Q.
Since the complete circle of the Smith Chart for Transmission Line, represents a half-wavelength along the line, a quarter-wavelength corresponds to a semicircle. It is not necessary to measure λ/4 around the circle from P, but merely to project the line through P and the center of the chart until it intersects the drawn circle at Q on the other side. (Although such an application is not very important in itself, it has been found of great value in familiarizing students with the chart and with the method of converting it for use as an admittance chart, this being essential for stub calculations.)
2. Calculation of the impedance or admittance at any point, on any transmission line, with any load, and simultaneous calculation of the SWR on the liner This may be done for lossless or lossy lines, but is much easier for lossless lines.
3. Calculation of the length of a short-circuited piece of transmission line to give a required capacitive or inductive reactance. This is done by starting at the point 0, j0 on the left-hand side rim of the chart, and traveling toward the generator until the correct value of reactance is reached. Alternatively, if a susceptance of known value is required, start at the right-hand rim of the chart at the point ∞,j∞ and work toward the generator again. This calculation is always performed in connection with short-circuited stubs.