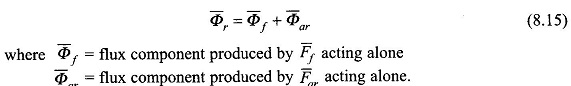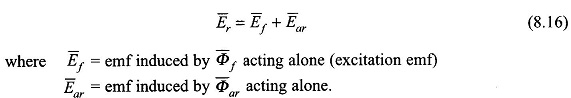Equivalent Circuit of Synchronous Motor:
By assuming linearity of the magnetic circuit, it is possible to obtain simple Equivalent Circuit of Synchronous Motor. The validity of this assumption stems from the fact that air-gap is the predominant component of the magnetic circuit of the machine.
As per Eq. (8.7), the resultant mmf phasor is given by
The resultant flux Φr and the air-gap emf Er must in general be obtained from Fr. However, the assumption of linear magnetic circuit (Φ = pF; p is constant permeance), allows one to find the resultant flux by the principle of superposition as
Since emf induced is proportional to the flux/pole (Eq. (8.6)) and lags behind it by 90°, from the flux phasor Eq. (8.15), the emf phasor equation can be written as
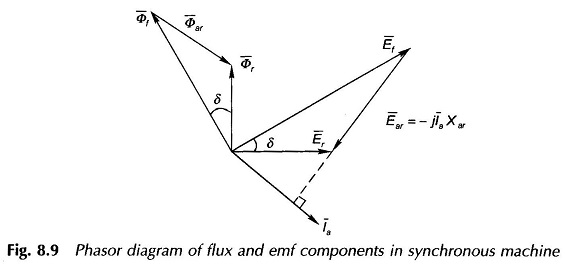
The emf phasors in Eq. (8.16) are proportional to the corresponding flux phasors of Eq. (8.15) with the emf phasors lagging the respective flux phasors by 90°. The phasor equations (8.15) and (8.16) are represented by the phasor diagram of Fig. 8.9. In this figure the flux phasor triangle and emf phasor triangle are similar to each other with the emf phasor triangle being rotated anticlockwise from the flux phasor triangle by 90°.
As Φar is in phase with Ia (generating machine) and is proportional to it, the emf Ear is proportional to Ia and lags behind it by 90°, i.e.
where Xar, the constant of proportionality, is indeed an inductive reactance. Thus Eq. (8.16) can be written as
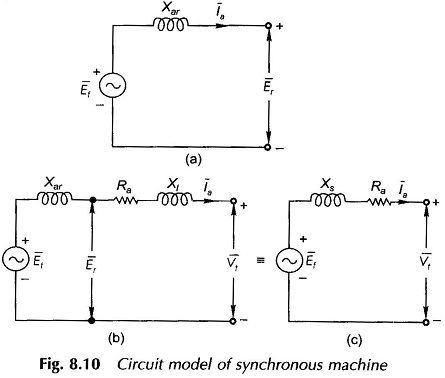
Corresponding to Eq. (8.18), Fig. 8.10(a) gives the per phase Equivalent Circuit of Synchronous Motor.
Comparing Eqs (8.15), (8.16) and (8.18), it is concluded that the reactance Xar equivalently replaces the effect of the armature reaction flux. If Xar is known for a machine, one can work in terms of voltages and currents and need not represent fluxes on the phasor diagram.
The effect of armature resistance Ra and leakage reactance Xl are embodied in the phasor equation as
From Eq. (8.19) and Fig. 8.10(a) follows the complete circuit model of Fig. 8.10(b) which can be reduced to the simpler form of Fig. 8.10(c) by combining series reactances and by allowing the identity of Er to be lost. In the circuit model of Fig. 8.10(c), the total reactance
is known as the synchronous reactance of the machine, while
is the synchronous impedance of the machine.
The synchronous reactance takes into account the flux produced by the flow of balanced 3-phase currents in the stator as well as the leakage flux. The excitation emf, Ef, accounts for the flux produced by the rotor field (dc excited). The magnitude of the excitation emf can be controlled by the dc field current (If) called the excitation current. If the load on the machine is thrown off, Ef appears at the machine terminals which then is the open-circuit volt age of the machine. With reference to Fig. 8.10(c) Ef is also called voltage behind synchronous impedance or reactance (as Ra can be neglected).
It must be remembered here that the synchronous impedance model of the synchronous machine is based on the linearity assumption and will hold for the unsaturated region of machine operation and is valid only for the cylindrical-rotor machine.
Range of Synchronous Impedance:
Expressed in the pu system, the synchronous reactance of synchronous machines lies in a narrow range of values. From practical data, it is observed that the armature resistance (Ra) is usually of the order of 0.01 pu, i.e. the voltage drop in the armature resistance at the rated armature current is about 1% of the rated voltage. The leakage reactance value ranges from 0.1 to 0.2 pu and the synchronous reactance (Xs = Xar + Xl) is of the order of 1.0 to 2 pu. It is, therefore, seen that the armature resistance of a synchronous machine is so low that it can be neglected for all practical purposes except in the computation of losses, temperature rise and efficiency. It may be noted here that Ra must be small in order to minimize the I2R loss and limit the temperature rise of the machine, and Xs should be large to limit the maximum current that may flow under fault (short-circuit) conditions. However, the modern practice is to design Equivalent Circuit of Synchronous Motor with a medium range of values for synchronous reactance as quick-acting circuit breakers are now available to disconnect a machine from the faulted line.