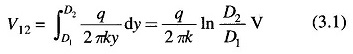Electric Field Inside a Conductor:
Imagine an infinitely long straight conductor far removed from other conductors (including earth) carrying a uniform charge of q coulomb/metre length. By symmetry, the equipotential surfaces will be concentric cylinders, while the lines of electrostatic stress will be radial. The Electric Field Inside a Conductor at a distance y from the axis of the conductor is
where k is the permittivity of the medium.
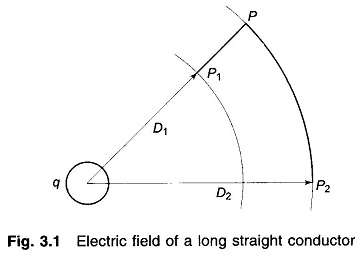
As shown in Fig. 3.1 consider two points P1 and P2 located at distances D1 and D2 respectively from the conductor axis. The potential difference V12 (between P1 and P2) is given by
As the potential difference is independent of the path, we choose the path of integration as P1PP2 shown in thick line. Since the path PP2 lies along an equipotential, V12 is obtained simply by integrating along P1P, i.e.