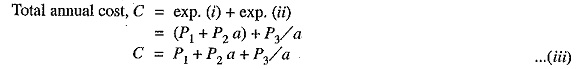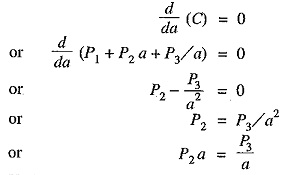Economic Choice of Conductor Size:

The cost of conductor material is generally a very considerable part of the total cost of a transmission line. Therefore, the determination of proper Conductor Size for the line is of vital importance. The most economical area of conductor is that for which the total annual cost of transmission line is minimum. This is known as Kelvin’s Law after Lord Kelvin who first stated it in 1881. The total annual cost of transmission line can be divided broadly into two parts viz., annual charge on capital outlay and annual cost of energy wasted in the conductor.

(I) Annual charge on capital outlay. This is on account of interest and depreciation on the capital cost of complete installation of transmission line. In case of overhead system, it will he the annual interest and depreciation on the capital cost of conductors, supports and insulators and the cost of their erection. Now, for an overhead line, insulator cost is constant, the conductor cost is proportional to the area of X-section and the cost of supports and their erection is partly constant and partly proportional to area of X-section of the Conductor Size. Therefore, annual charge on an overhead’ transmission line can be expressed as :

where P₁ and P₂ are constants and a is the area of X-section of the conductor.

(ii) Annual cast of energy wasted. This is on account of energy lost mainlyt in the conductor due to /²R losses. Assuming a constant current in the conductor throughout the year, the energy lost in the conductor is proportional to resistance. As resistance is inversely proportional to the area of X-section of the Conductor Size, therefore, the energy lost in the conductor is inversely proportional to area of X-section. Thus, the annual cost of energy wasted in an overhead transmission line can be expressed as :

where P₃ is a constant.

In exp. (iii), only area of X-section a is variable. Therefore, the total annual cost of transmission line will be minimum if differentiation of C w.r.t. a is zero i.e.

i.e.Variable part of animal charge = Annual cost of energy wasted

Therefore Kelvin’s Law can also be stated in an another way i.e. the most economical area of conductor is that for which the variable part of annual charge is equal to the cost of energy losses

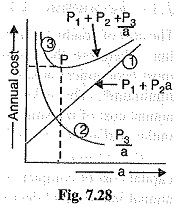
Graphical illustration of Kelvin’s law. Kelvin’s law can also be illustrated graphically by plotting annual cost against X-sectional area ‘a’of the conductor as shown in Fig. 7.28. In the diagram, the straight line (1) shows the relation between the annual charge (i.e., P₁ + P₂a) and area of X-section a of the conductor. Similarly, the rectangular hyperbola (2) gives the relation between annual cost of energy wasted and X-sectional area a. By adding the ordinates of curves (1) and (2), the curve (3) is obtained. This latter curve shows the relation between total annual cost (P₁+P₂a+P₃/a) transmission line and area of X-section a. The lowest point on the curve (i.e., point P) represents the most economical area of X-section.

Limitations of Kelvin’s law. Although theoretically Kelvin’s law holds good, there is often considerable difficulty in applying it to a proposed scheme of power transmission. In practice, the limitations of this law are :

• It is not easy to estimate the energy loss in the line without actual load curves, which are not available at the time of estimation.
• The assumption that annual cost on account of interest and depreciation on the capital outlay is in the form P₁ + P₂a is strictly speaking not true. For instance, in cables neither the cost of cable dielectric and sheath nor the cost of laying vary in this manner.

• This law does not take into account several physical factors like safe current density, me­chanical strength, corona loss etc.
• The Conductor Size determined by this law may not always be practicable one because it may be too small for the safe carrying of necessary current.
• Interest and depreciation on the capital outlay cannot be determined accurately.