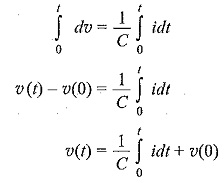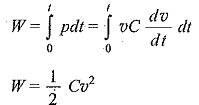Capacitance Formula:
Capacitance Formula is given by any two conducting surfaces separated by an insulating medium exhibit the property of a capacitor. The conducting surfaces are called electrodes, and the insulating medium is called dielectric. A capacitor stores energy in the form of an electric field that is established by the opposite charges on the two electrodes.
The electric field is represented by lines of force between the positive and per unit voltage that is capacitor can store is its capacitance, denoted by C.
what is the unit of capacitance?
The unit of capacitance is Farad denoted by F. By definition, one Farad is the amount of capacitance when one coulomb of charge is stored with one volt across the plates.
Capacitor Symbol:
The symbol for capacitance is shown in Fig. 1.5.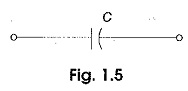
A capacitor is said to have greater capacitance if it can store more charge per unit voltage and the Capacitance Formula is given by
(lower case letters stress instantaneous values)
We can write the above equation in terms of current as
where
- v is the voltage across capacitor
- i is the current through it
Integrating both sides, we have
where v(0) indicates the initial voltage across the capacitor.
From the above equation, the voltage in a capacitor is dependent upon the integral of the current through it, and the initial voltage across it.
The power absorbed by the capacitor is given by
The energy stored by the capacitor is
From the above discussion we can conclude the following
- The current in a capacitor is zero if the voltage across it is constant; that means, the capacitor acts as an open circuit to dc.
- A small change in voltage across a capacitance within zero time gives an infinite current through the capacitor, which is physically impossible. In a fixed capacitance the voltage cannot change abruptly.
- The capacitor can store a finite amount of energy, even if the current through it is zero, and
- A pure capacitor never dissipates energy, but only stores it; that is why it is called non-dissipative passive element. However, physical capacitors dissipate power due to internal resistance.