Transmission Zero:
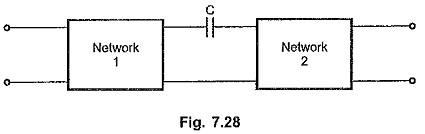
The Transmission Zero functions describe the transmission of signal from one end to other end. The Fig. 7.28 shows the transfer of signal from one network to other through a capacitor C.
There is a transmission through the capacitor producing finite output for finite input, at all the frequencies. But at s = 0 i.e. at zero frequency, the capacitor reactance becomes infinite and it acts as open circuit. There can not be any output, though there is finite input at zero frequency. Thus s = 0 is called zero of transmission for this network.
The frequencies at which, zero output results for a finite input are called zeros of transmission. At these frequencies Transmission Zero results. The zeros of T.F. T(s), which are the critical frequencies, are the zeros of transmission for the network described by that transfer function T(s). So a zero of transmission is a zero of transfer function.
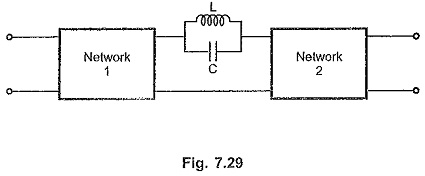
Consider the network shown in the Fig. 7.29.
The transmission is through LC parallel circuit. For ideal L and C the impedance of the parallel resonant circuit is ∞. It acts as open circuit at a resonant frequency of 1/√LC
Now if finite input is applied at ωr = 1/√LC, then LC resonant circuit acts as open circuit which results into Transmission Zero. Thus the zeros of transmission for this networks are s = ± j 1/√LC.
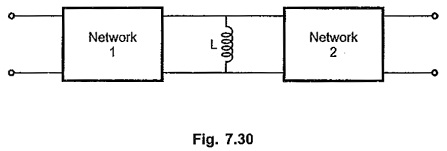
Consider another network shown in the. Fig. 7.30.
The impedance of the reactance is sL. At zero frequency, it acts as short circuit. Hence zero output results for finite input at zero frequency. Hence zero of transmission is at s =0 for an inductor in shunt arm.
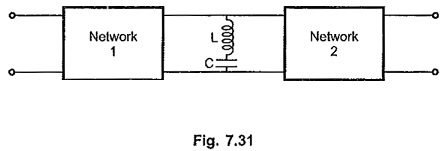
Consider a network with LC series network as transmitting network as shown in the Fig. 7.31. For ideal L and C, as resonant frequency ωr = 1/√LC, the impedance of LC series resonant circuit is zero. It acts as short circuit, producing zero output.
For such a network, the zeros of transmission are at s = ± j 1/√LC.
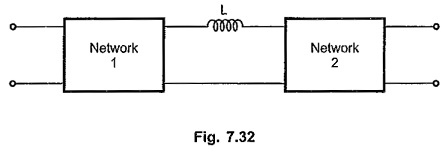
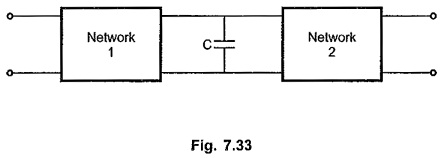
Consider the networks shown in the Fig. 7.32 and Fig. 7.33 with inductor in series arm and capacitor in shunt arm respectively.
At s = ∞, the inductor acts as open circuit and capacitor acts as short producing zero output. Hence the zero of transmission is at s = co for both these networks.
In general, zeros of transmission are zeros of the transfer function. All the transfer functions Z12,Z21,Y21 etc have the same zeros of transmission except in some special cases.
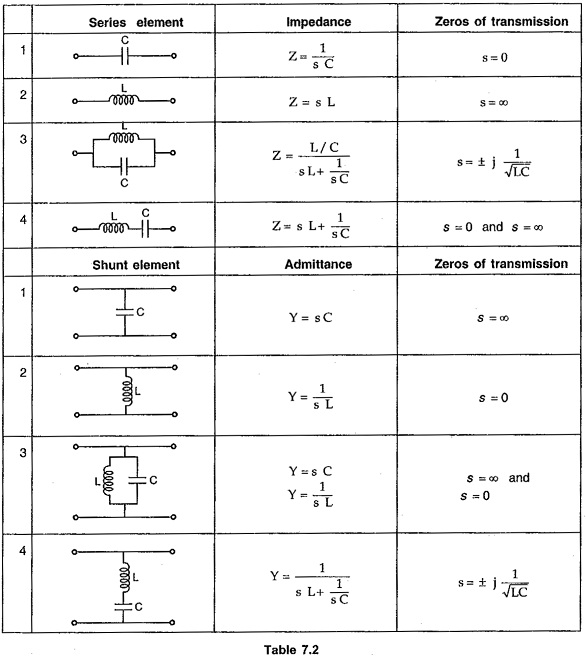
The table 7.2 gives possible combinations of elements and the corresponding Transmission Zero.
Minimum phase functions : The transfer function having zeros of transmission only on the jω axis or in the left half of s plane, is called minimum phase function.
Non-minimum phase functions : The transfer function having one or more zeros of transmission in right half of s plane is called non-minimum phase function.
Any transfer function of a passive ladder network is always minimum phase function.