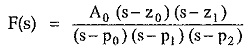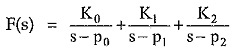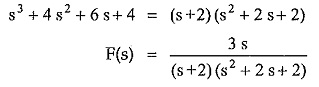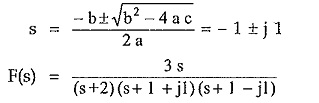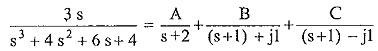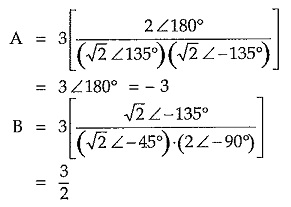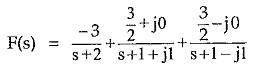Evaluation of Residue Using Pole-zero Plot:

The behavior of a network can be predicted only by looking at the pole-zero plot. The poles are the complex frequencies explaining the time responses. Also zeros are useful in finding partial fraction expansion. In this section, we will discuss graphical methods for obtaining the residue i.e. partial-fraction expansion coefficients directly from the pole-zero plot.

Consider the network function as follows,

Then we can expand F(s) as,

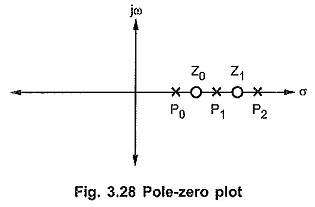
The poles and zeros are plotted on the complex plane as shown in the Fig. 3.28.

The residue K at any pole p is equal to the ratio of product of the vectors from the zeros to that pole to the product of the vectors from the other poles to that pole.

Note that the residues of the conjugate poles are also conjugate in nature.

With the help of ruler and protractor angles of the vectors so that residues can be determined. Consider following function,

For finding partial expansion, factorize the denominator by general method, we get

Finding roots of s² + 2 s + 2 = 0 by the formula,

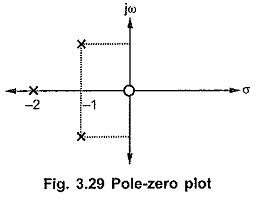
The pole zero plot is as follows, shown in the Fig. 3.29.

The partial fractions can be written as,

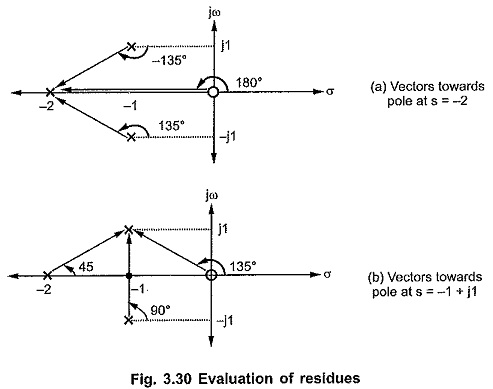
To find A, draw vectors from other poles and zeros. Find magnitude and angle with +ve real axis of all vectors.

Note that for the function given, scale factor K= 3. The vectors drawn from zeros must be written in numerator while those from poles in denominator.

Similarly C = 3/2, as we have seen already that residues of complex conjugate poles are also conjugate in nature.