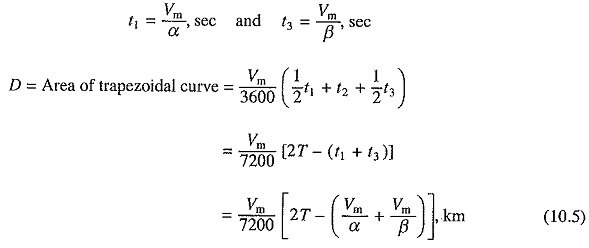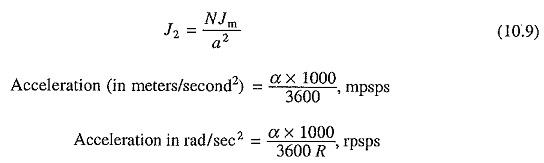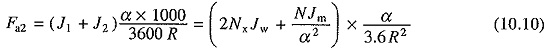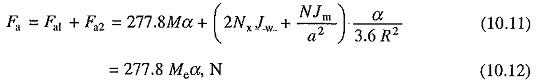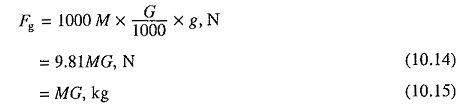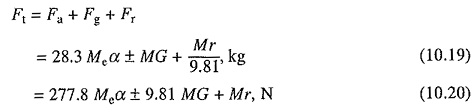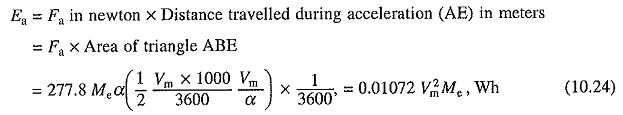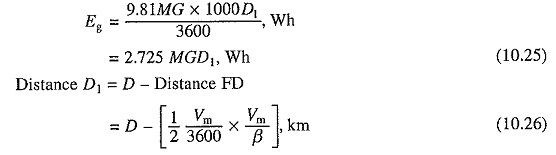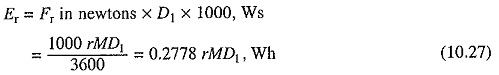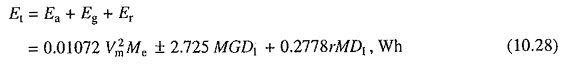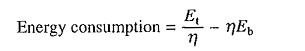Traction Drive Rating and Energy Consumption:
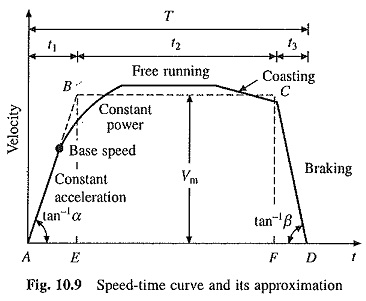
Traction Drive Rating and Energy Consumption – The speed-time curve of Fig. I0.6(a) is reproduced in Fig. 10.9. For simplification in calculations, it is approximated by a trapezoidal curve having constant values for acceleration and deceleration. As the area beneath curve represents distance covered, the area of trapezoidal curve is chosen equal to the area of actual curve.
Let D be the distance in km, T the time taken by train to move from A to D in sec, Vm the free running speed of trapezoidal curve in km/hr (kmph) and α, β = acceleration/deceleration in km/hr/sec (kmphps).
From the trapezoidal curve,
Eq. (10.5) has five variables D, Vm T, α and β. If any four are known, the fifth can be evaluated.
Tractive Effort and Traction Drive Rating:
Tractive effort is the force developed at the rims of driving wheels for moving train. In main line trains it is caused by locomotive and in suburban by motor coaches. Draw bar pull is the force exerted by locomotive through draw bar for moving train. Thus, draw bar pull is less than tractive effort by the force required to move the locomotive. The tractive effort has to perform following functions:
- Accelerate the train mass horizontally.
- Accelerate the rotating parts of train such as wheels, gears, axles and the rotor of the
- Overcome force due to gravity when moving up-gradient.
- Overcome train resistance.
1. Tractive effort required to accelerate the train mass horizontally (in newtons) at an acceleration of α kmphps is
where M is the mass in tonnes.
2. Tractive effort required to accelerate the rotating parts: Rotating parts consists of wheels, axles, gears and rotor of the motor. The inertia of gears and axles can be ignored in comparison to that of wheels. Moment of inertia of wheels
where Jw is the moment of inertia of one wheel, kg-m2 and Nx the number of axles on the train.
Let
N = number of driving motors
n1 = teeth on motor gear wheel
n2 = teeth on axle gear wheel
R = radius of the wheel, m
Jm = moment of inertia of one motor, kg-m2
Then moment of inertia of motors referred to wheels
Tractive effort for driving rotating parts
Total tractive effort required for accelerating the train on a level rack (in newtons)
where Mc is defined as the effective mass of the train. It accounts for rotating parts in addition to the train mass. It is around 8-15% higher than M. Equation (10.12) can also be written as
3. Tractive effort required to overcome force due to gravity: When moving up-gradient, the drive has to produce tractive effort to overcome force due to gravity. When deciding Traction Drive Rating, gradient with the maximum permissible slope is to be considered. In railway practice, gradient is expressed as rise in meters in a track distance of 1000 m and is denoted by G.
Now, tractive effort required to overcome force due to gravity will be
4. Tractive effort required to overcome train resistance: Variation of train resistance with speed is shown in Fig. 10.4. It is not possible to accurately represent it analytically. Among several empirical relations proposed, the simplest is based on the understanding that train resistance is due to various kinds of frictions. Therefore, it will have three basic components: one due to coulomb friction which is independent of speed, second will be due to viscous friction which is proportional to speed, and third because of air friction which is proportional to speed squared. Thus,
where V is the speed of the train, and A, B, C are constants. Eq. (10.16) suggests that it is difficult to estimate the train resistance. Since it is quite small compared to Fa, an approximate value of Fr can be used and is often assumed as r newtons per tonne weight of the train. Thus,
For calculating Traction Drive Rating, r is chosen to be 20 N/tonne.
5. Total tractive effort required to move the train
The positive sign is used for the train movement up-gradient and negative for down the gradient.
Motor torque rating:
Total torque at the rims of driving wheels = Total tractive effort (in newtons) X R![]() where R is the radius of the driving wheels in meters.
where R is the radius of the driving wheels in meters.
Total torque referred to the motor shaft
where ηt is the efficiency of transmission.
Torque per motor
where N is the number of motors.
When deciding motor rating, maximum gradient allowed while laying down the track should be considered.
Specific Energy Consumption:
An estimate of energy required to operate train is needed so that running expenses can be calculated. To facilitate these calculations the term specific energy consumption has been defined as the energy consumed in watt-hours per tonne of train weight and per kilometer of distance travelled. The energy output at the driving axles is spent to:
- Accelerate the train.
- Overcome the gradient.
- Overcome the train resistance.
Energy output at the driving axles to accelerate the train (Ea)
Assuming trapezoidal speed-time curve of Fig. 10.9
Energy output at the driving axles to overcome the gradient (Eg)
where D1 is the distance in km for which the power remains on. From the trapezoidal curve this distance is AF which is equal to the area ABCF. Thus
Energy output at the driving axles to overcome the train resistance (Er)
Total energy output at the driving axles (Et)
Specific energy output in Wh per tonne per km = Et/MD, Whptpkm
Specific energy consumption
where η is the efficiency of transmission and motor.
When regenerative braking is used, energy regenerated is fed back to the source, thus reducing specific energy consumption. Proceeding as above, we obtain energy output at the driving axle Eb as follows:
where Vb is the initial speed during braking, + ve sign is for up-gradient and -ve for down gradient (for second term on right side only).
Assuming transmission system and motor efficiency to be the same during motoring and braking
Specific energy consumption
Maximum Allowable Tractive Effort:
The maximum tractive effort that can be applied without wheel slip
where μ is the coefficient of adhesion and Md the adhesive weight or weight on the driving wheels.