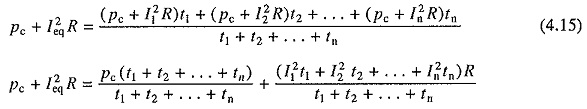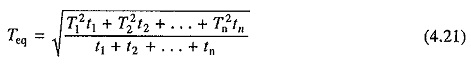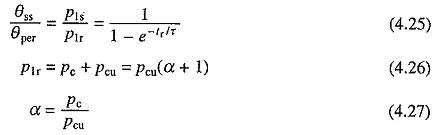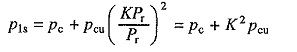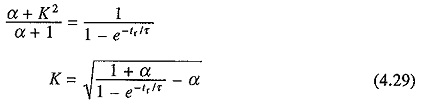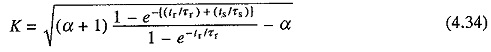Motor Rating Various Duty Cycles:
From the point of view of calculation of motor rating various Motor Rating Various Duty Cycles can be broadly classified as:
-
Continuous duty.
-
Fluctuating loads.
-
Short-time and intermittent duty.
Continuous Duty:
Maximum continuous power demand of the load is ascertained. A motor with next higher power rating from commercially available ratings is selected. Obviously, motor speed should also match load’s speed requirements. It is also necessary to check whether the motor can fulfil starting torque requirement and can continue to drive load in the face of normal disturbances in power supply system; the latter is generally assured by the transient and steady-state reserve torque capacity of the motor.
Equivalent Current, Torque and Power Methods for Fluctuating and Intermittent Loads:
This method can be employed for duties (iii)-(viii). It is based on approximation that the actual variable motor current can be replaced by an equivalent Ieg which produces same losses in the motor as actual current. This equivalent current is determined as follows:
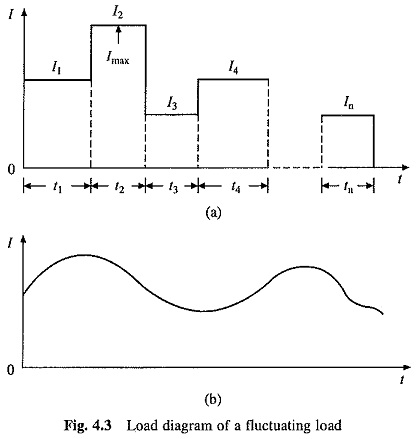 Motor loss P1 consists of two components constant loss Pc which is independent of load and consists of core-loss and friction loss; and load dependent copper loss. Thus for a fluctuating load (Fig. 4.3(a)) consisting of n values of motor currents I1,I2, . . . , In for duration t1,t2, . . . ,tn respectively, the equivalent current Ieq is given by
Motor loss P1 consists of two components constant loss Pc which is independent of load and consists of core-loss and friction loss; and load dependent copper loss. Thus for a fluctuating load (Fig. 4.3(a)) consisting of n values of motor currents I1,I2, . . . , In for duration t1,t2, . . . ,tn respectively, the equivalent current Ieq is given by
If the current varies smoothly over a period T (Fig. 4.3(b)), Eq. (4.16) can be written as
Implicit in above analysis is the assumption that heating and cooling conditions remain same. If motor runs at a constant speed throughout this operation, heating and cooling conditions will, in fact, remain same. If speed varies, constant losses will marginally change. However, if forced ventilation is used, heating and cooling conditions can still be assumed to remain same without much loss of accuracy. In self ventilating machines, cooling conditions at low speeds will be poorer than at normal speed. Consequently Eqs. (4.16) and (4.17) should be used with caution.
After Ieq is determined, a motor with next higher current rating (= Irated) from commercially available ratings is selected. Next, this rating is checked for its practical feasibility as follows:
DC Motor:
This motor can be allowed to carry larger than the rated current for a short duration. This is known as short time overload capacity of the motor. A normally designed dc machine is allowed to carry up to 2 times the rated current (3 to 3.5 times the rated current in specially designed dc machines) because for higher currents sparking between the brushes and commutator reaches an unacceptable level. Let the ratio of maximum allowable current (or short time overload current capacity) to rated current be denoted by λ. Then
where Imax is the maximum value of current (Fig. 4.3) and Irated is the rated current of the motor. If condition (4.18) is not satisfied then the motor current rating is calculated from
Induction and Synchronous Motors:
In case of induction and synchronous motors, for stable operation, maximum load torque should be well within the breakdown torque of the motor. If motor current rating selected based on Eqs. (4.16) or (4.17) violates this constraint, the Motor Rating Various Duty Cycles is selected to satisfy breakdown torque constraint. In case of induction motors with normal design, the ratio of breakdown to rated torque varies from 1.65 to 3 and for synchronous motors 2 to 2.25 (for special types up to 3.5). If the ratio of breakdown to rated torque is denoted by λ′ then the motor torque rating is chosen based on
When the load has high torque pulses, selection of Motor Rating Various Duty Cycles based on this will be too large. Load equalization by mounting a flywheel on the motor shaft must then be considered.
Equivalent current method assumes ‘constant losses‘, to remain constant for all operating points. Therefore, this method should be carefully employed when these losses vary. It is also not applicable to motors with frequency (or speed) dependent parameters of the equivalent circuit, e.g. in deep-bar and double squirrel-cage rotor motors the rotor winding resistance and reactance vary widely during starting and braking making this method inapplicable.
When torque is directly proportional to current, as for example in de separately excited motor, then from Eq. (4.16),
Equation (4.21) can be employed to directly ascertain the motor torque rating.
When motor operates at nearly fixed speed, its power will be directly proportional to torque. Hence, for nearly constant speed operation, power rating of the motor can be obtained directly from:
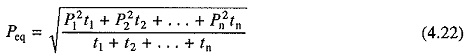 Short Time Duty:
Short Time Duty:
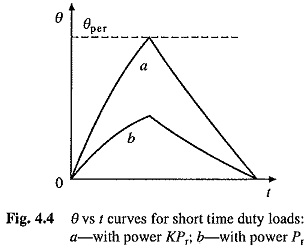
In short time duty, time of motor operation is considerably less than the heating time constant and motor is allowed to cool down to the ambient temperature before it is required to operate again. If a motor with a continuous duty power rating of Pr is subjected to a short time duty load of magnitude Pr, then the motor temperature rise will be far below the maximum permissible value θper and the motor will be highly underutilized (Fig. 4.4). Therefore, motor can be overloaded by a factor K(K > 1) such that the maximum temperature rise just reaches the permissible value θper as shown in Fig. 4.4.
When the duration of running period in a Motor Rating Various Duty Cycles with power KPr is tr, then from Eq. (4.9)
Note that θss is the steady state temperature rise which will be attained if motor delivers a power (KPr) on continuous basis, whereas the permissible temperature rise θper is also the steady state temperature rise attained when motor operates with a power Pr on continuous basis. If the motor losses for powers Pr and (KPr) be P1r and P1s, respectively, then from Eq. (4.7)
and Pc is the load independent (constant) loss and Pcu the load dependent loss. Then
Substituting from Eq. (4.27)
Substituting from Eqs. (4.26) and (4.28) into Eq. (4.25) gives
Equation (4.29) allows the calculation of overloading factor K which can be calculated when constant and copper losses are known separately. When separately not known, total loss is assumed to be only proportional to (power)2, i.e. α is assumed to be 0.
As already mentioned, K is subjected to the constraints imposed by maximum allowable current in case of dc motors and breakdown toruqe limitations in case of induction and synchronous motors.
Intermittent Periodic Duty:
During a period of operation, if the speed changes in wide limits, leading to changes in heating and cooling conditions, methods of equivalent current, torque or power, described in the previous section cannot be employed. This section describes methods useful for such cases.
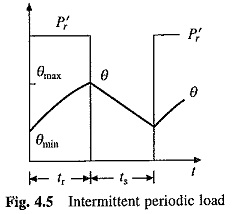
Let us consider a simple intermittent load, where the motor is alternately subjected to a fixed magnitude load P′r of duration tr and standstill condition of duration ts (Fig. 4.5). As motor is subjected to a periodic load, after the thermal steady-state is reached the temperature rise will fluctuate between a maximum value θmax and a minimum value θmin. For this load, the Motor Rating Various Duty Cycles should be selected such that θmax ≤ θper, where θper is the maximum permissible temperature rise of the motor.
From Eq. (4.6), temperature at the end of working (or running) interval will be given by
and fall in temperature rise at the end of standstill interval ts will be
where τr and τs are the thermal time constants of motor for working and standstill intervals. Combining Eqs. (4.30) and (4.31) yields![]()
For full utilization of motor, θmax = θper. Further θper will be the motor temperature rise when it is subjected to its continuous rated power Pr. Form Eq. (4.7), ratio θss/θmax will be proportional to losses that would take place for two values of load. If losses for load values Pr and P′r be denoted by P1r and P1s, then
From Eqs. (4.26), (4.28), (4.32) and (4.33), overloading factor K (= P′r / Pr) is given by
K can be determined from Eq. (4.34) subject to maximum current limitation of dc motors and breakdown torque constraints of induction and synchronous motors. As explained earlier, when constant and copper losses are not available separately, α is replaced by zero in Eq. (4.34).