Polar Curve in illumination | Rousseau’s Construction:

Polar Curve in illumination – All discussions made so far were based on the assumption that the luminous intensity or the candle power from a source is uniformly distributed over the surrounding surface. But none of the practical type of lamp provides light uniformly distributed in all directions because of its un-symmetrical shape. It is often necessary to know the distribution of light in various directions to ascertain how the candle power of a light source varies in different directions. The luminous intensity in all the directions can be represented by polar curves.

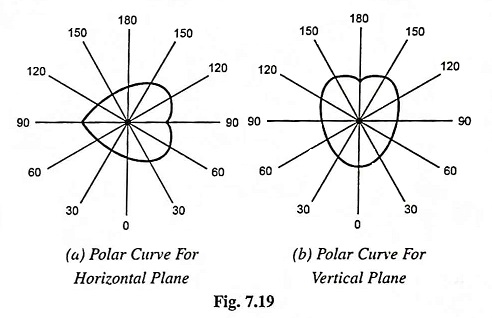
If the luminous intensity in a horizontal plane passing through the lamp is plotted against angular position, a curve known as horizontal polar curve is obtained. If the luminous intensity in a vertical plane is plotted against the angular position, a curve known as vertical polar curve is obtained. The typical polar curves for an ordinary filament lamp are shown in Fig. 7.19.

The polar curves are used to determine the mean horizontal candle power (mhcp) and mean spherical candle power (mscp). These are also used to determine the actual illumination of a surface by employing the candle power in that particular direction as read from the vertical polar curve in illumination calculations.

The mean horizontal candle power of a lamp can be determined from the horizontal polar curve by taking the mean value of the candle power in a horizontal direction.

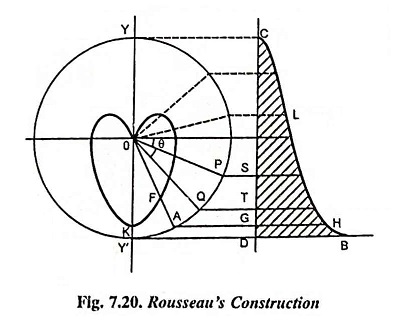
Mean spherical candle power can be determined from the vertical polar curve by Rousseau’s construction.

Rousseau’s Construction:

The construction is illustrated in Fig. 7.20. A semicircle of any convenient radius is drawn with the pole of the polar diagram as centre. The line CD is drawn equal and parallel to the vertical diameter YY′. Now from this line CD ordinate equal to corresponding radius on the polar curve are set up such as DB = OK, GH = OF and so on. The curve obtained by joining the ends of these ordinates is known as Rousseau’s curve. The mean ordinate of this curve gives the mscp of the lamp having polar curve given in the Fig. 7.20.

The area under the curve can either be determined on a graph paper or found by Simpson’s rule.