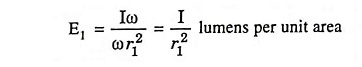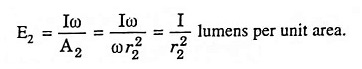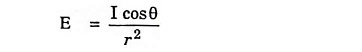Laws of illumination in Electrical:
There are two laws of illumination
- Law of inverse squares and
- Lambert’s cosine law.
Law of Inverse Squares:
If a source of light which emits light equally in all directions be placed at the centre of a hollow sphere, the light will fall uniformly on the inner surface of the sphere, that is to say, each square mm of the surface will receive the same amount of light. If the sphere be replaced by one of the larger radius, the same total amount of light is spread over a larger area proportional to the square of the radius. The amount which falls upon any square mm of such a surface will, therefore, diminish as the radius increases, and will be inversely proportional to the square of the distance.
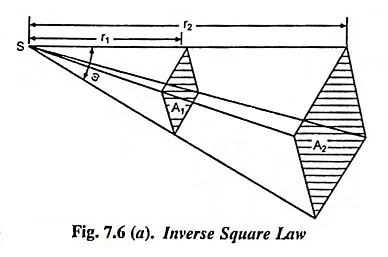
A similar relation holds if we have to deal with a beam of light in the form of a cone or pyramid, as shown in Fig. 7.6 (a). If we consider parallel surfaces which cut the pyramid at different distances from the source, the areas of these surfaces are proportional to the square of these distances, and, therefore, the amount of light which falls on one unit of the area of these surfaces, is inversely proportional to the square of the distance from the source. This relationship is referred to as the law of inverse squares.
Mathematically it can be proved as follows :
Let us consider surface area A1 and surface area A2 at distances r1 and r2 respectively from the point source S of luminous intensity I and normal to the rays, as shown in Fig. 7.6 (a).
Let the solid angle subtended be ω steradians
Luminous flux radiated per steradians = I
Total luminous flux radiated = Iω lumens
Illumination on the surface of area A1
and area A1 = ωr12
Illumination on the surface of area A1,
Similarly illumination on the surface of area A2,
Hence the laws of illumination of a surface is inversely proportional to the square of the distance between the surface and the light source provided that the distance between the surface and the source is sufficiently large so that the source can be regarded as a point source.
Lambert’s Cosine Law:
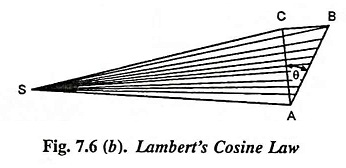
Very often the illuminated surface is not normal to the direction of light as AC in Fig. 7.6 (b) but is inclined as AB.
The area over which the light is spread is then increased in the ratio
and the illumination decreases in the ratio cosθ/1.
The expression for the illumination then becomes
According to this laws of illumination at any point on a surface is proportional to the cosine of the angle between the normal at that point and the direction of luminous flux.