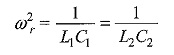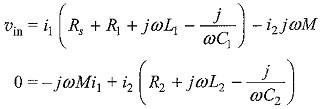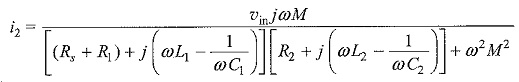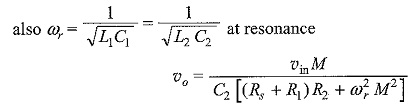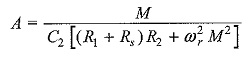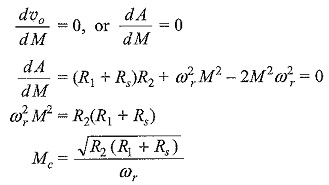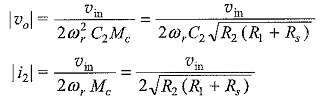Doubled Tuned Coupled Circuits:

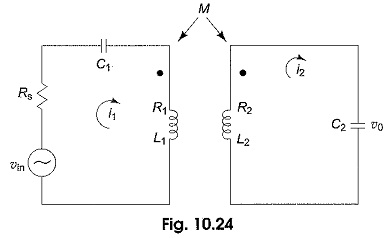
Figure 10.24 shows a Doubled Tuned Coupled Circuits involving two series resonant circuits.

For the circuit shown in the figure, a special case where the primary and secondary resonate at the same frequency ω_r, is considered here,

i.e.

The two mesh equations for the circuit are

From which

or

where A is the amplification factor given by

The maximum amplification or the maximum output voltage can be obtained by taking the first derivative of υ_o with respect to M, and equating it to zero.

where M_c is the critical value of mutual inductance. Substituting the value of M_c in the equation of υ_o we obtain the maximum output voltage as

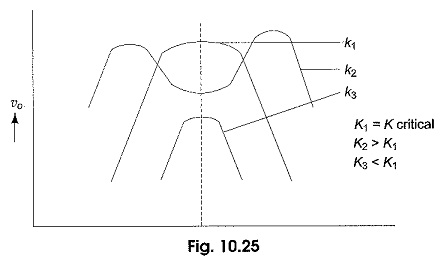
By definition, M = K√L₁L₂, the coefficient of coupling, K at M = M_c is called the critical coefficient of coupling, and is given by K_c = M_c/√L₂L₁.

The critical coupling causes the secondary current to have the maximum possible value. At resonance, the maximum value of amplification is obtained by changing M; or by changing the coupling coefficient for a given value of L₁ and L₂. The variation of output voltage with frequency for different coupling coefficients in Doubled Tuned Coupled Circuits is shown in Fig. 10.25.