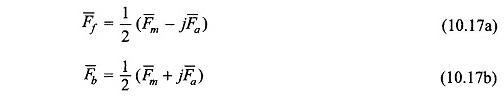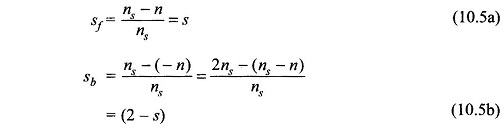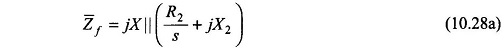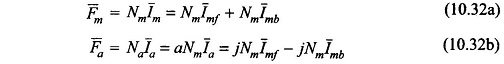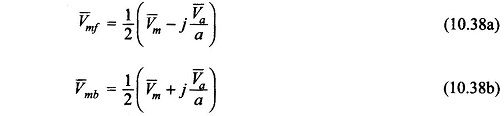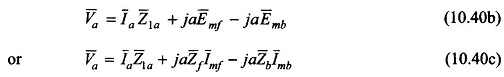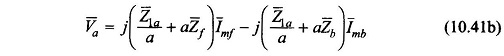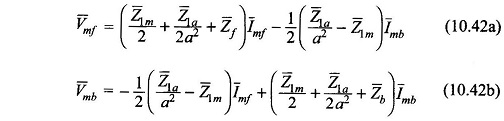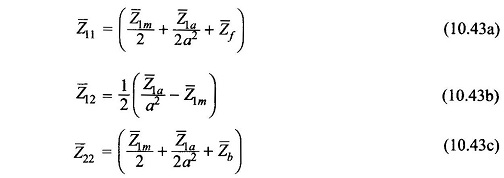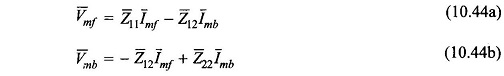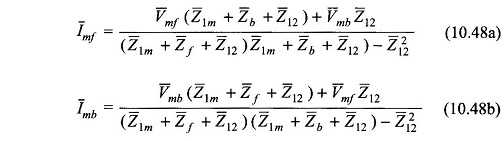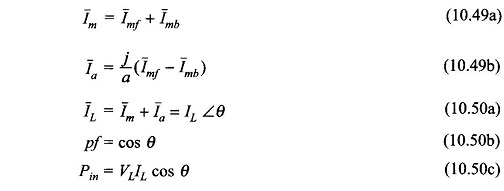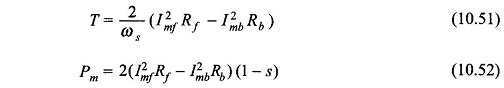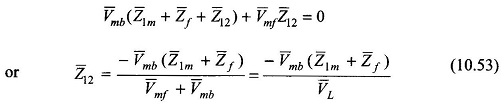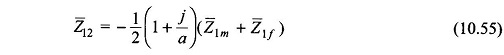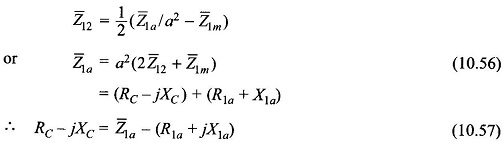Equivalent Circuit of Single Phase Induction Motor

Equivalent Circuit of Single Phase Induction Motor:

Equivalent Circuit of Single Phase Induction Motor – The winding unbalance and the fact that both the main and auxiliary windings are fed by the same supply result in unbalanced main and auxiliary fields. The phasor along the winding axes can be split into symmetrical components F̅_f and F̅_b as given by Eqs (10.17a) and (10.17b). The forward component set F̅_f and jF̅_f produces a forward rotating field; similarly the backward component set F̅_b and -jF̅_b results in a backward rotating field.

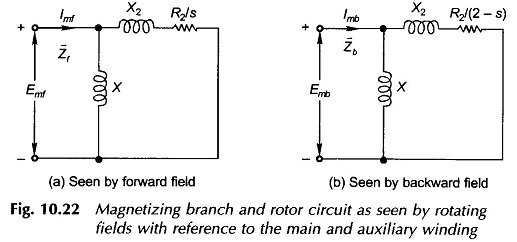
The rotor slips with respect to the two rotating fields are s and (2 – s) respectively as given by Eqs (10.5a) and (10.5b) and as a result the magnetizing and rotor circuits as seen by the two rotating fields with reference to the main winding are different and are shown in Figs 10.22(a) and 10.22(b).

It is noted that no-load losses have been neglected and therefore the core-loss conductance has not been shown in both the circuits. The impedance seen by E_mf, the forward field induced emf of the main winding, is

and the impedance seen by the E_mb,backward field induced emf in the main winding, is

Hence

and

where

I̅_mf= forward component current in main winding
I̅_mb= backward component current in main winding

Of course

Equations (10.16a) and (10.16b) will now be converted into current form.

Let

N_m= equivalent number of main windings turns

N_a= equivalent number of auxiliary winding turns

Define

Then from Eqs (10.16a) and (10.16b)

From Eqs (10.32a) and (10.32b)

The current in the auxiliary winding is I̅_abut since the turns of auxiliary and main winding are different , the auxiliary winding current as seen from the main winding is equal to

From Eqs (10.33a) and (10.33b) the symmetrical components of mail and auxiliary winding currents with reference to the min winding can be expressed as

The forward field reaches the auxiliary winding 90° elect. ahead of the main winding and vice versa for the backward rotating field. Thus the emf’s in the auxiliary winding induced by the two fields are:

Also let the main and auxiliary winding terminal voltages be V̅_m and V̅_a respectively. The auxiliary winding voltage is equal to (V_a/a) as seen from the main winding. This set of voltages can also be split into symmetrical components as

or alternatively

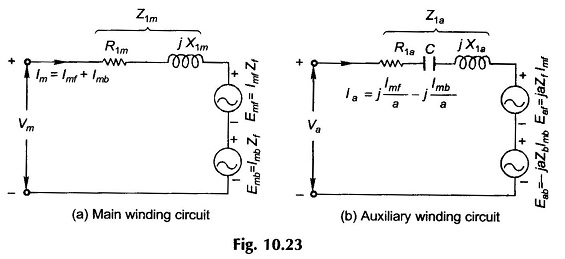
Now consider the main winding terminal voltage V̅_m. It comprises three components: the emf induced by the forward rotating field, the emf induced by backward rotating field and the voltage drop in the winding impedance Z̅_1m owing to current I_m flowing through it. Thus

Substituting for E̅_mf and E̅_mb from Eqs (10.29a) and (10.29b)

which is represented by the Equivalent Circuit of Single Phase Induction Motor of Fig. 10.23(a).

Similarly the auxiliary winding terminal voltage V̅_a comprises three components,

i.e.

where Z̅_1a is the winding impedance of the auxiliary winding which in general has a capacitor included in it (starting/running capacitor). Using Eqs (10.36a) and (10.36b),

whose Equivalent Circuit of Single Phase Induction Motor representation is given in Fig. (10.23b).

Substituting I_m from Eq. (10.33a) in Eq. (10.39b),

Similarly substituting I_a from Eq. (10.33b) in Eq. (10.40c),

With V̅_m and V̅_a as expressed in Eqs (10.41a) and (10.41b), one obtains from Eqs (10.38a) and (10.38b)

Defining

Equations (10.42a) and (10.42b) can be written as

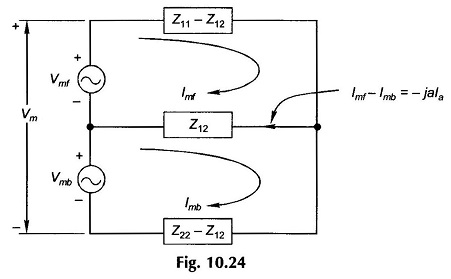
Equations (10.44a), (10.44b) and (10.37a) are represented by the Equivalent Circuit of Single Phase Induction Motor of Fig. 10.24.

It is further noted that

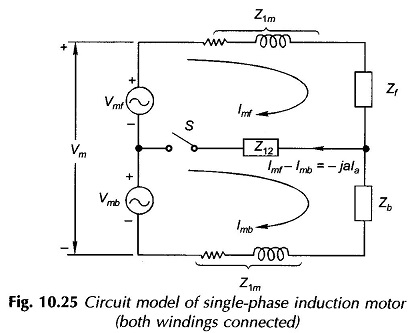
From these the Equivalent Circuit of Single Phase Induction Motor of Fig. 10.24 can be drawn in the form of Fig.10.25. In Fig. 10.25 disconnecting the auxiliary winding under running condition is equivalently represented as the opening of switch S.

Once the auxiliary Winding is disconnected.

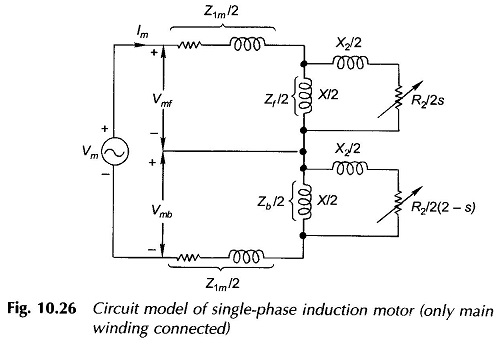
By doubling the current and reducing the impedance to half the circuit model of Fig. 10.26 is obtained. It may be seen that this is the same circuit model as already presented in Fig. 10.5(c) on a heuristic basis.