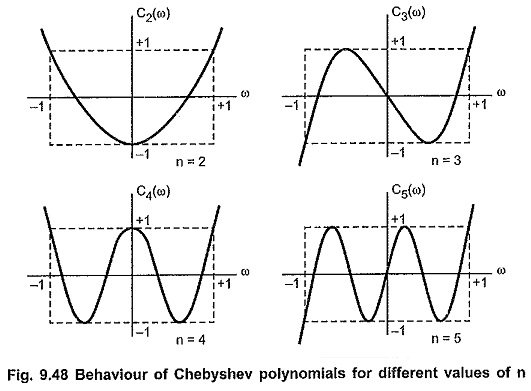
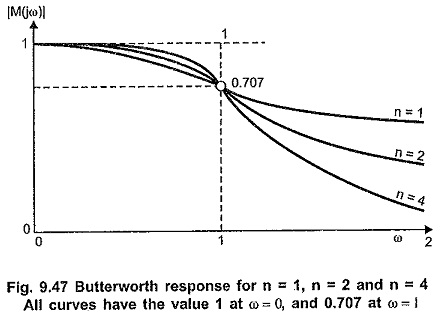
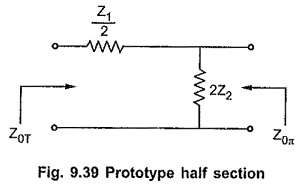
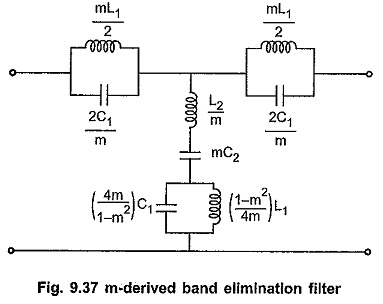
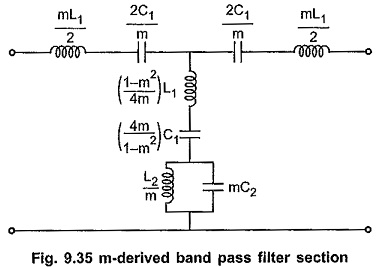
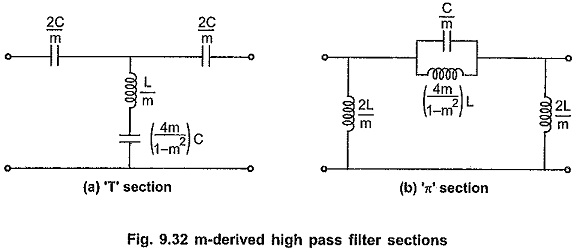
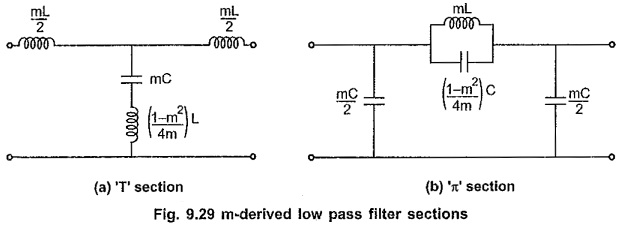
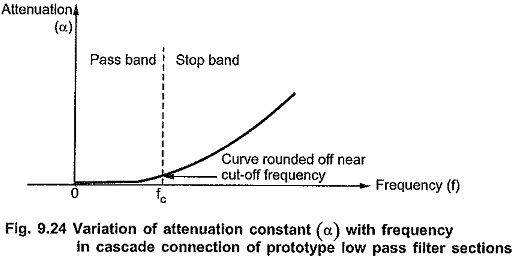
Chebyshev Approximation
Chebyshev Approximation: Chebyshev Approximation - In the earlier section, we have studied that the Butterworth approximation is the best at ω = 0. But as we move towards cut-off frequency, ωc = 1, approximation becomes poorer.…