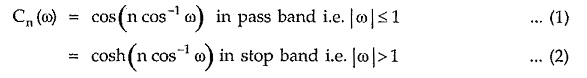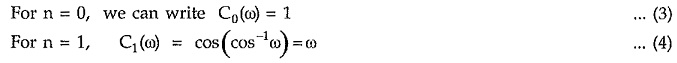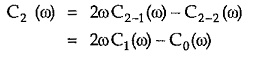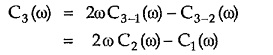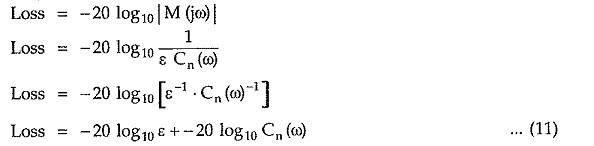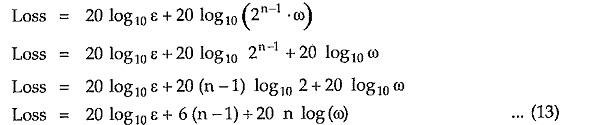Chebyshev Approximation:

Chebyshev Approximation – In the earlier section, we have studied that the Butterworth approximation is the best at ω = 0. But as we move towards cut-off frequency, ω_c = 1, approximation becomes poorer. It departs from ideal characteristics.

Let us consider an approximation which “ripples” about the normalized magnitude, unity, in the pass band and magnitude decreases very rapidly beyond cut-off frequency in stop band. This Chebyshev approximation is equally good at ω = 0 and ω = 1. So the approximation is also called equal ripple approximation.

Equal ripple property is obtained by using Chebyshev cosine polynomials defined as,

Let us find Chebyshev cosine polynomials for different values of n.

Higher order Chebyshev polynomials are obtained by using recursive formula,

Thus for n = 2, we get C₂(ω)

Substituting values of C₁(ω) and C₀(ω) from equation (4) and (3) respectively, we get

For n = 3, we get C₃(ω) as

Substituting values of C₁(ω) and C₂(ω) from equations (4) and (6) respectively, we get,

The Chebyshev polynomials for different values of n are as given in the Table 9.11.

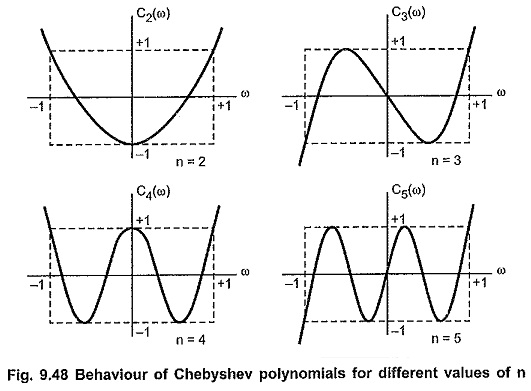
The behaviour of Chebyshev polynomials with the variation of ω is as shown in Fig. 9.48.

Some important properties of Chebyshev polynomials useful in low-pass filter approximation are as follows :

1. From the plots of Chebyshev polynomials, it is clear that the zeros of the polynomials are located in the interval ω = – 1 to ω = 1, that is, |ω| ≤ 1.
2. Within the interval from ω = -1 to ω = 1, the magnitude of Chebyshev polynomial is always less than or equal to unity, that is, |C_n(ω)|≤1 for |ω|≤1.
3. Outside interval lei |ω|≤1, magnitude of Chebyshev polynomial rapidly increases with increase in ω.

After the summary of few properties of Chebyshev polynomials, let us study how to use Chebyshev polynomials in low-pass filter approximation. Consider the function ε² C²_n(ω) where ε is the real number which is very small compared to unity. As seen from above properties ε² C²_n(ω) will vary between 0 and ε² is the interval |ω|≤1 as C₁(ω) = 1. Let us add 1 to this function making it 1 + ε² C²_n(ω). This new function will vary between 1 and 1+ε² for |ω|≤1 where (1 + ε²) is slightly greater than 1. Inverting this new function and relating it to the square of the magnitude we get

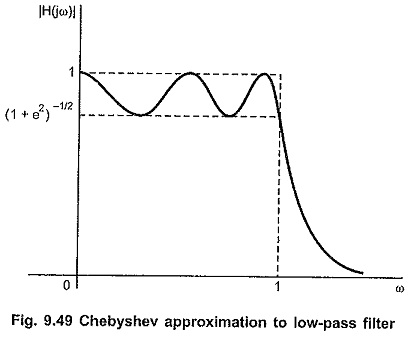
In the interval fro |ω|≤1 i.e. in the pass band, the square of the magnitude will oscillate or ripple about a unity such that maximum value is 1 while minimum is 1/(1+ε²) Outside interval |ω|≤1 i.e. stop band, C²_n(ω) becomes very large such that |M(jω)|² approaches zero very rapidly with increase in co. Hence it is most suitable for ideal low pass filter characteristics.

The Chebyshev approximation to the ideal low-pass filter is as shown in Fig. 6.49.

Within the pass band 0 ≤ ω ≤ 1, the magnitude M (jω) oscillates or ripples between 1 and √1+ε². The distance between maximum and minimum in the pass band is called ripple height and it is given by,

In the stop band, that is, for |ω|≥1, as ω increases, ε²C²_n(ω) becomes very large as compared to 1 then

In the stop band, the loss or attenuation expressed in dB is given by

But for large ω, C_n(ω) can be expressed as,

Substituting value of C_n(ω) from equation (12) in the expression for loss,

From above expression it is observed that Chebyshev response falls of at the rate of 20 n dB/decade after initial loss of [20 log₁₀ ε + 6 (n —1)] dB.

In most of the applications ε is very small, which gives 20 log ε term negative. Thus it is necessary to compensate this decrease in the loss in the stop band. To achieve this, a filter of sufficiently higher order is selected.

Basically Chebyshev approximation depends upon two variables namely ε and n. These two values can be determined directly from the specifications given for the filter. The value of ε is determined from maximum permissible ripple. Once the value of ε is fixed, value of n can be found from the required attenuation in stop band.