Balanced Three Phase Circuit:

The solution of a balanced three phase circuit is easily carried out by solving the single-phase network corresponding to the reference phase.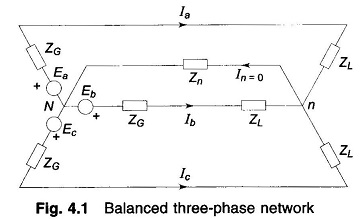

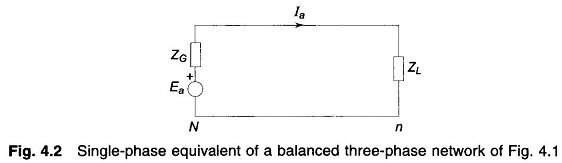
Figure 4.1 shows a simple, balanced three phase circuit. The generator and load neutrals are therefore at the same potential, so that I_n = 0. Thus the neutral impedance Z_n does not affect network behavior. For the reference phase a

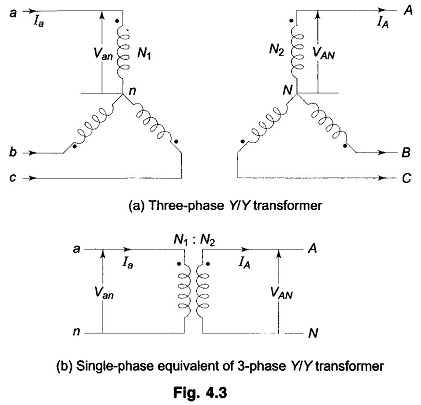
The currents and voltages in the other phases have the same magnitude but are progressively shifted in phase by 120°. Equation (4.1) corresponds to the single-phase network of Fig. 4.2 whose solution completely determines the solution of the balanced three phase circuit.

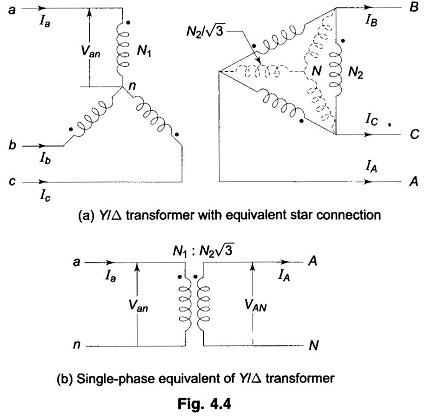
Consider now the case where a three-phase transformer forms part of a three-phase system. If the transformer is Y/Y connected as shown in Fig. 4.3a, in the single-phase equivalent of the three-phase circuit it can be obviously represented by a single-phase transformer (as in Fig. 4.3b) with primary and secondary pertaining to phase a of the three-phase transformer.

If the transformer is Y/Δ connected as in-Fig. 4.4a, the delta side has to be replaced by an equivalent star connection as shown dotted so as to obtain the single-phase equivalent of Fig. 4.4b. An important fact has, however, to be observed here. On the delta side the voltage to neutral V_AN and line current I_A have a certain phase angle shift from the star side values V_an and I_a (90° for the phase labelling shown). In the single-phase equivalent (V_AN, I_A) are respectively in phase with (V_an, I_a). Since both phase voltage and line current shift through the same phase angle from star to delta side, the transformer per phase impedance and power flow are preserved in the single-phase equivalent.

In most analytical studies, we are merely interested in the magnitude of voltages and currents so that the single-phase equivalent of Fig. 4.4b is an acceptable proposition. Wherever proper phase angles of currents and voltages are needed, correction can be easily applier after obtaining the solution through a single-phase transformer equivalent.

It may be noted here that irrespective of the type of connection, the transformation ratio of the single-phase equivalent of a three-phase transformer is the same as the line-to-line transformation ratio.