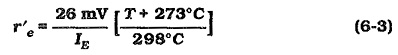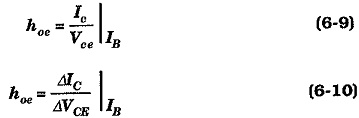Transistor Models and Parameters:

T-Equivalent Circuit – Because a transistor consists of two pn-junctions with a common centre block, it should be possible to use two pn-junction ac equivalent circuits as the Transistor Models and Parameters. Figure 6-9 shows the ac equivalent circuit for a transistor connected in common-base configuration. Resistor r_e represents the BE junction resistance, r_c represents the CB junction resistance, and r_b represents the resistance of the base region which is common to both junctions. Junction capacitances C_BE and C_BC are also included.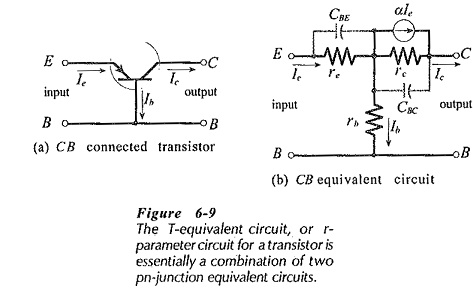

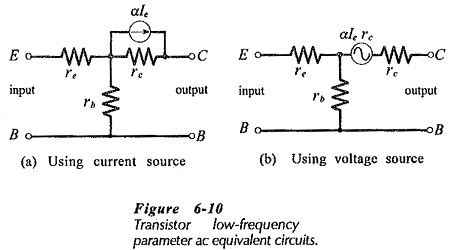
If the Transistor Models and Parameters equivalent circuit is simply left as a combination of resistances and capacitances, it could not account for the fact that most of the emitter current flows out of the collector terminal as collector current. To represent this, a current generator is included in parallel with r_c and C_BC. The current generator is given the value αI_e, where, α = I_c/I_e.

The complete circuit is known as the T-equivalent circuit, or the r-parameter equivalent circuit. The equivalent circuit can be rearranged in common-emitter or common-collector configuration.

The currents in Fig. 6-9 are designated I_b, I_c, and I_e (instead of I_B,I_C, and I_E) to indicate that they are ac quantities rather than dc. The circuit parameters r_c, r_b, r_e, and α, are also ac quantities.

r-Parameters:

Referring to Fig. 6-9, r_e represents the ac resistance of the forward-biased BE junction, so it has a low resistance value, (typically 25 Ω). The resistance of the reverse-biased CB junction (r_c) is high, (typically 100 kΩ to 1 MΩ). The base region resistance (r_b) depends upon the doping density of the base material. Usually, r_b ranges from 100 Ω to 300 Ω.

C_BE is the capacitance of a forward-biased pn-junction, and C_BC is that of a reverse-biased junction. At medium and low frequencies the junction capacitances may be neglected. Instead of the current generator (αI_e) in parallel with r_c, a voltage generator (αI_er_c) may be used in series with r_c. Two transistor r-parameter models are shown in Fig. 6-10.

Determination of r_e:

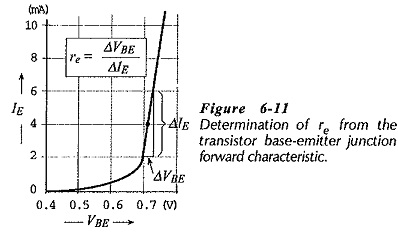
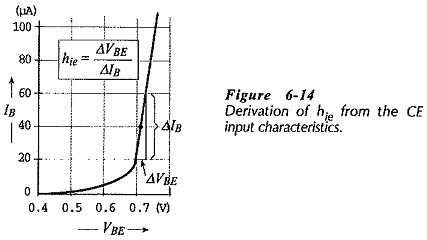
Because r_e is the ac resistance of the BJT forward-biased base-emitter junction, it can be determined from a plot of I_E versus V_BE. As illustrated in Fig. 6-11,

This is similar to the determination of the dynamic resistance (r_d) for a forward-biased diode. Also like the case of a diode, the ac resistance for the transistor BE junction can be calculated in terms of the current crossing the junction.

As in the case of r′_d for a diode, r’_e does not include the resistance of the device semiconductor material. Consequently, r’_e is slightly smaller than the actual measured value of r_e for a given transistor.

Equation 6-2 applies only to transistors at a temperature of 25°C. For determination of r’_e at higher or lower temperatures, the equation must be modified.

h-Parameters:

It has been shown that Transistor Models and Parameters circuits can be represented by an r-parameter or T-equivalent circuit. In circuits involving more than a single transistor, analysis by r-parameters can be virtually impossible. The hybrid parameters, or h-parameters are much more convenient for circuit analysis. These are used only for ac circuit analysis, although dc current gain factors are also expressed as It-parameters. Transistor h-parameter models simplify transistor circuit analysis by separating the input and output stages of a circuit to be analyzed.

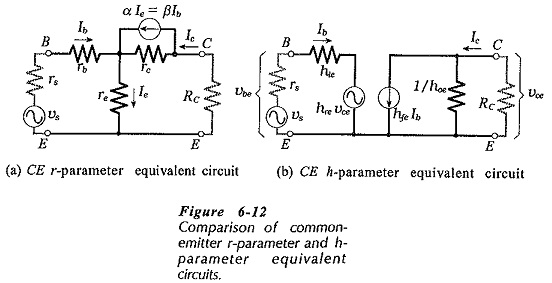
In Fig. 6-12 a common-emitter h-parameter equivalent circuit is compared with a common-emitter r-parameter circuit. In each case an external collector resistor (R_C) is included, as well as a signal source voltage (v_s) and source resistance (r_s). Note that the output current generator in the r-parameter circuit has a value of αI_e, which equals βI_b.

The input to the h-parameter circuit is represented as an input resistance (h_ie) in series with a voltage source (h_reυ_ce). Looking at the r-parameter circuit, it is seen that a change in output current I_c causes a voltage variation across r_e. This means that a voltage is fed back from the output to the input. In the h-parameter circuit this feedback voltage is represented as the portion h_re of the output voltage υ_ce. The parameter h_re is appropriately termed the reverse voltage transfer ratio.

The output of the h-parameter circuit is represented as an output resistance (1/h_oe) in parallel With a current generator (h_feI_b), where I_b is the (input) base current. So, h_feI_b is produced by the input current I_b, and it divides between the device output resistance 1/h_oe and the collector resistor R_C. I_c is the current passed to R_C. This compares with the r-parameter equivalent circuit, where some of the generator current (βI_b) flows through r_c. The current generator parameter (h_fe) is termed the forward transfer current ratio. The output conductance is h_oe, so that 1/h_oe is a resistance.

r_π Equivalent Circuit:

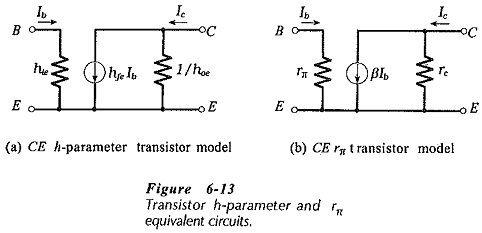
An approximate h-parameter model for a transistor CE circuit is shown in Fig. 6-13(a). In this case, the feedback generator (h_reυ_ce in Fig. 6-12(b)) is omitted. The effect of h_reυ_ce is normally so small that it can be neglected for most practical purposes.

The approximate h-parameter circuit is reproduced in Fig. 6-13(b) with the components labelled as r-parameters; r_π = h_ie, βI_b = h_feI_b, and r_c =1/h_oe. This circuit, known as a hybrid-π model, is sometimes used instead of the h-parameter circuit.

Definition of h-Parameters:

The e in the subscript of h_ie identifies the parameter as a common-emitter quantity, and the i signifies that it is an input resistance. Common-base and common-collector input resistances are designated h_ib and h_ic, respectively.

As an ac input resistance, h_ie can be defined as the ac input voltage divided by the ac input current.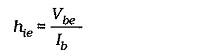

This is usually stated as,

This means that the collector-emitter voltage (V_CE) must remain constant when h_ie is measured.

The input resistance can also be defined in terms of changes in dc levels;

Equation 6-5 can be used for determining h_ie from the transistor common-emitter input characteristics. As illustrated in Fig. 6-14, ΔV_BE and ΔI_B are measured at one point on the characteristics, and h_ie is calculated.

The reverse transfer ratio h_re can also be defined in terms of ac quantities, or as the ratio of dc current changes. In both cases, the input current (I_B) must be held constant.

The forward current transfer ratio h_fe can similarly be defined in terms of ac quantities, or as the ratio of dc current changes. In both cases, the output voltage (V_CE) must be held constant.

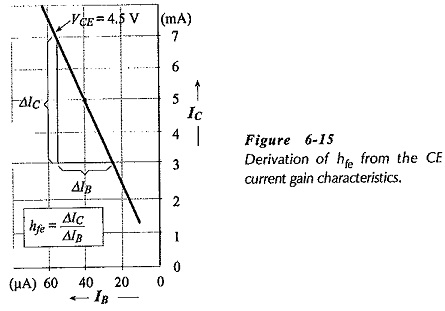
Equation 6-8 can be used to determine h_fe from the CE current gain characteristics. Figure 6-15 shows the measurement of ΔI_C and ΔI_B at one point on the characteristics for the h_fe calculation.

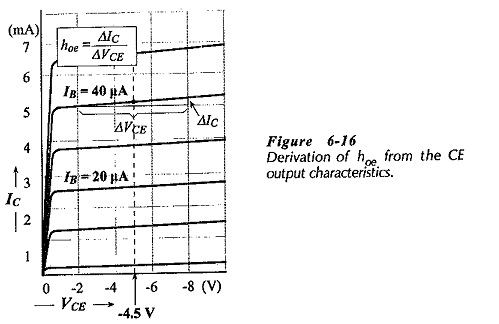
The output conductance, h_fe, is the ratio of ac collector current to ac collector-emitter voltage, and its value can be determined from the common emitter output characteristics (see Fig. 6-16).

Common-Base and Common-Collector h-Parameter:

The common-base and common-collector h-parameters are defined similarly to common-emitter h-parameters. They may also be derived from the CB and CC characteristics. Common-base parameters are identified as h_ib, h_fb, etc., and common-collector parameters are designated h_ic, h_fc, and so on.

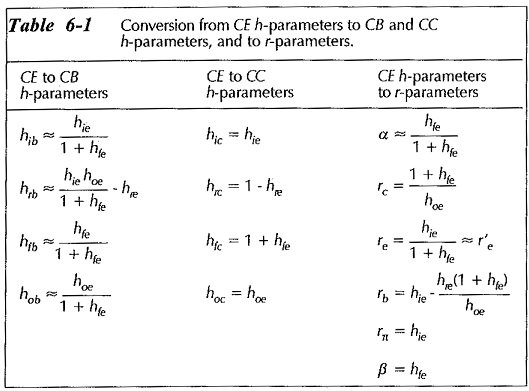
Parameters Relationships:

Device manufacturers do not list the values of all parameters on transistor data sheets. Usually, only the CE h-parameters are stated. However, CB and CC h-parameters can be determined from the CE h-parameters. r-parameters can also be calculated from the CE h-parameters. Table 6-1 shows the parameter relationships.