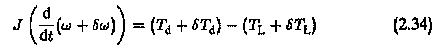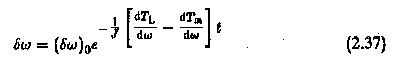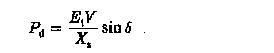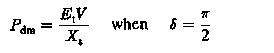Transient stability in Electrical Drives:

Transient stability in Electrical Drives – From the preceding discussion it is clear that a drive is in its state of equi­librium at constant speed if the developed motor torque is equal to the sum of load torque and friction. The basis of the investigation of the dynamics of a drive from one steady-state equilibrium condition to another has already been discussed in detail. Electrical drives have closed loop control systems. Investigations on the stability of drives must include all the controls available along with the motor and mechanical system. A system is in an equilibrium condition, if there is no disturbance. In the presence of a disturbance the equilibrium conditions are disturbed and the drive tries to take a new equilib­rium position under the new input conditions. The system is said to be stable if sometime after the appearance of a disturbance it attains a new equilibrium condition. The system is said to be unstable if it comes to rest or has a continuous increase in speed following the disturbance. i.e. the system is unable to take up a new equilibrium position. The disturbances may be external or internal to the drive.

The stability of a drive may be affected very much by the parameters of controllers, motors, etc. A system which is stable for one set of parameters may become unstable for another set. The stability investigations of a drive system having closed loop controls and represented by means of a block diagram will be discussed in detail in a later chapter dealing with the control techniques of drives.

The stability of a drive is influenced by the inertia of the rotating masses and inductances of the motor, in the same manner as the transient behaviour. Therefore in cases of sudden changes of parameter causing the drive to change its equilibrium state, the effects of these components cannot be ignored. The stability behaviour of the drive taking into account the effects of these param­eters is called Transient stability in Electrical Drives. On the other hand, if the changes from one state of equilibrium to another take place too slowly to have the effects of the above parameters, the stability conditions refer to steady-state stability.

Before discussing the stability characteristics of a drive in a closed loop or open loop operation it is first necessary to investigate the stability of the motor driving the load. The motors have both steady-state and Transient stability in Electrical Drives conditions existing in them.

Stability Behaviour of Electrital Machines—Steady State Stability

The nature of response of an electrical machine between two states of equi­librium following a disturbance, which would also refer to the nature of its stability, can be obtained by solving the differential equations of the motor along with the dynamic equation of motion. The time response so obtained gives information regarding the transient response as well as stability. The mo­tor is stable if the transient portion of the response dies down with time. As the equations are non-linear they are linearised using the method of small sig­nals about an operating point. These equations give operating point stability. This tedious investigation is necessary to get an insight into the steady-state stability and to develop criteria for it in cases of disturbances. Stability studies can be easily done using the steady-state speed-torque curves assuming that in cases of disturbances the operating point moves along these curves.

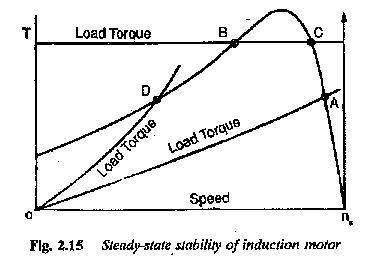
The steady-state stability can be explained with reference to Fig. 2.15, in which some typical speed-torque curves of a motor and load are shown. Con­sider the situation at point A. A small decrease in speed is followed by an increase in the motor torque which accelerates the load and brings it back to the equilibrium point. Note also that after the disturbance has occurred, the motor torque is greater than the load torque. In reaching the point of equilibrium, the drive may overshoot it, with further increase in speed. The motor torque decreases and becomes smaller than the load torque. Under these conditions no more acceleration is possible and the drive retards. It finally comes to a state of equilibrium after several oscillations. In the case of an induction motor the oscillations are effectively damped out by the induced currents in the squirrel cage. The motor successfully returns to its original point of equilibrium in case of a small increase in speed also. It is stable at point A. T_L > T_d following an increase in speed which effectively brakes the motor.

Consider the operation at B. A small decrease in speed decreases the torque developed by the motor. Further, from the figure we see that the load torque is greater than the torque developed by the motor. This causes further retardation. The process being cumulative, the motor finally comes to rest. If there is a small increase in speed, the developed torque increases, which accelerates the load torque. This process is also cumulative and the speed goes on increasing the motor does not return to its original operating point. Point B is unstable.

Following the reasoning given for point A, the operation at point C is stable. At point D, even though the torque developed decreases with decrease in speed it is able to accelerate the load, because T_d > T_L. The motor reaches its original point of operation. It is also a stable point.

Taking these discussions into consideration, it can be concluded that the motor is stable if the change in motor torque following a decrease in speed is such that it is greater than the load torque, or smaller than the load torque following an increase in speed.

In the foregoing discussions, the load torque is constant at the operating point. If in a motor-load combination a change in speed can bring about changes in the motor as well as load torques, stable operation can be envisaged only if the change in the load torque is greater (smaller) than the change in the motor torque in case of an increase (decrease) in speed. In the former case excess load torque has a tendency to brake the motor, whereas in the latter case excess motor torque has a tendency to accelerate the rotor so that the system is stable again.

These conclusions can also be drawn on the basis of the dynamic equation of motion applied to the operating point.

Let the motor be operating at a developed torque T_d and a load torque T_L. The speed of operation is ω. Let there be small variations of δT_L and δT_d following a speed variation δω. Before the disturbance occurs we have

After the disturbance we have

From these equations we get

This can be written as

Solving this equation we get

where (δω) is the initial disturbance in speed. The speed transient can be obtained from Eq. 2.37. The transient will die down to zero if

making the exponential term decrease with time. When this condition is satisfied, the motor returns to its original operating point and the machine is said to be stable. Else, the speed transient increases continuously and the machine is unstable.

From the condition given in Eq. 2.38 we can conclude that a machine is stable if its load speed-torque curves are such that for

• a decrease in speed, the motor torque is greater than the load torque.
• an increase in speed, the load torque is greater than the motor torque.

From the condition it can also be seen that a decrease (increase) in speed must bring about a greater (smaller) change in the motor torque than in the load torque so that the machine can be accelerated (retarded) under the influence of the motor torque (load torque) to its original point of operation.

The steady-state stability criterion discussed above assumes that the deviations in speed and torque follow the steady-state speed-torque curves of the motor and load. Also, the changes are so slow that the energy storage elements, such as inertia and inductance, do not affect the variation while going from one state of equilibrium to the other. However, if the changes are very fast the effects of these parameters cannot be ignored. In that case the results of steady-state stability are optimistic. A machine which is stable in the steady-state may lose its stability under transient conditions when the effects of inertia are considerable. A motor can be loaded to its maximum capacity of torque or power when it is slowly or gradually loaded. For transient type of loads the motor cannot reach this limit because of kinetic energy of the rotating parts also has to be considered, Therefore the stability information during transient con­ditions is different from steady-state stability information. A machine which can be loaded to its maximum power under steady-state conditions may not be loaded to the same extent under transient loading conditions.

A knowledge of Transient stability in Electrical Drives is essential for the proper design of flywheel and other associated controls.

In a synchronous motor drive, the steady-state speed and torque of the motor and load may be such that the steady-state stability criterion does not provide any reliable information regarding its stability. Therefore it is neces­sary to study its Transient stability in Electrical Drives.

It is well known that a synchronous motor is very sensitive to sudden changes of load and prone to what is called hunting.

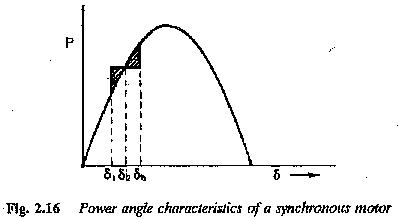
(The oscillatory behaviour of a rotor about a mean torque angle position is called hunting.) The nature of hunting can be discussed with reference to the power angle characteristic shown in Fig. 2.16.

The power developed by synchronous motor, neglecting armature resistance is

assuming a cylindrical rotor. Under a steady-state this may reach a maximum value

which cannot, however, be reached under transient conditions. Let the ma­chine be operating at a power angle equal to δ, giving a power of P. The torque balance equation may be replaced by the power balance equation due to the constancy of speed. The power developed in the motor is equal to the load power and damping power. The latter may be neglected while deriving the criteria for Transient stability in Electrical Drives.

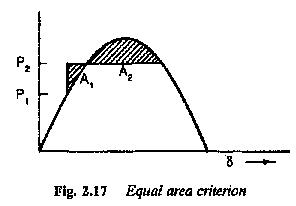
When a load is suddenly applied to the shaft of a synchronous motor there is a momentary slowing down of the motor. This causes the rotor to fall back from its old position in order to develop the required torque. Till the rotor attains its new position the rotor releases the kinetic energy to drive the increased load during retardation. The rotor angle increases to a value where sufficient torque is developed to drive the load. At this position ro­tor speed is less than synchronous speed. The rotor does not remain at this new equilibrium position. It has to be brought back to its synchronous speed by replenishing the kinetic energy released by the rotating mass. Therefore the torque angle increases further. The torque developed is more than the load torque. Excess torque accelerates the rotor and eventually reduces the torque angle. The rotor may overshoot the equilibrium position. The rotor thus oscillates like a torsional pendulum about the equilibrium position corresponding to new torque. The motor operation is stable when the torque angle changes within π/2 However, during oscillations or hunting of the motor there is a possibility that the motor has a torque angle greater than π/2. The motor may be stable or may lose its stability. In such cases the stability of the drive can be estimated using equal area criterion. Referring to Fig. 2.17, δ_o is the load angle before the load is applied. δ_m is the mean position of oscillation and δ_f, is the final value of torque angle during oscillation. For the machine to retain stability and remain in synchronism the value of A₂≥A₁. If A₂<A₁ the motor loses its synchronize.