Refraction of Waves:
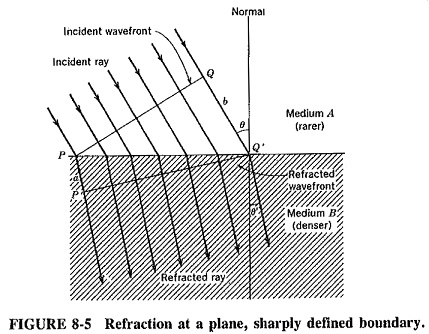
As with light, Refraction of Waves takes place when electromagnetic waves pass from one propagating medium to a medium having a different density. This situation causes the wavefront to acquire a new direction in the second medium and is brought about by a change in wave velocity. The simplest case of refraction, concerning two media with a plane, sharply defined boundary between them, is shown in Figure 8-5.
Consider the situation in Figure 8-5, in which a wave passes from medium A to the denser medium B, and the incident rays strike the boundary at some angle other than 90°. Wavefront P-Q is shown at the instant when it is about to penetrate the denser medium, and wavefront P’-Q’ is shown just as the wave has finished entering the second medium. Meanwhile, ray b has travelled entirely in the rarer medium, and has covered the distance Q-Q’ , proportional to its velocity in this medium. In the same time ray a, which travelled entirely in the denser medium, has covered the distance P-P’. This is shorter than Q-Q’ because of the lower wave velocity in the denser medium. The in-between rays have travelled partly in each medium and covered total distances as shown; the wavefront has been rotated.
The relationship between the angle of incidence Band the angle of Refraction of Waves θ may be calculated with the aid of simple trigonometry and geometry. Considering the two right-angled triangles PQQ’ and PP’Q, we have
Therefore
where
νA = wave velocity in medium A
νB = wave velocity in medium B
It will be recalled, from Equation (7-7) and the accompanying work, that the wave velocity in a dielectric medium is inversely proportional to the square root of the dielectric constant of the medium. Substituting this into Equation (8-8) gives
where
k = dielectric constant of medium A
k’ = dielectric constant of medium B
μ = refractive index
Note, once again, that the dielectric constant is exactly 1 for a vacuum and very nearly 1 for air.
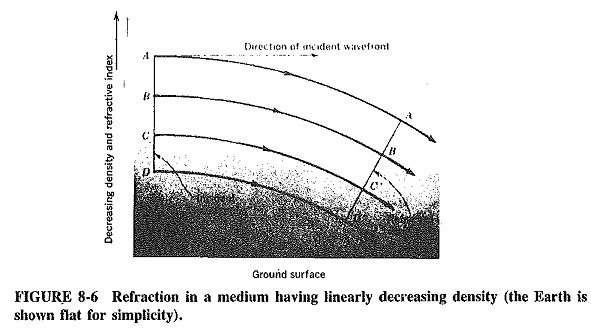
When the boundary between the two media is curved, Refraction of Waves still takes place, again following the optical laws. If the change in density is gradual, the situation is more complex, but refraction still takes place. Just as Figure 8-5 showed that electromagnetic waves travelling from a rarer to a denser medium are refracted toward the normal, so we see that waves travelling the other way are bent away from the normal. However, if there is a linear change in density (rather than an abrupt change), the rays will be curved away from the normal rather than bent, as shown in Figure 8-6.
The situation arises in the atmosphere just above the earth, where atmospheric density changes (very slightly, but linearly) with height. As a result of the slight Refraction of Waves that takes place here, waves are bent down somewhat instead of travelling strictly in straight lines. The radio horizon is thus increased, but the effect is noticeable only for horizontal rays. Basically, what happens is that the top of the wavefront travels in rarer atmosphere than the bottom of the wavefront and therefore travels faster, so that it is bent downward. A somewhat similar situation arises when waves encounter the ionosphere.