Standing Waves in Transmission Lines:
Standing Waves in Transmission Lines : When power is applied to a transmission line by a generator, a voltage and a current appear whose values depend on the characteristic impedance and the applied power. The voltage and current waves travel to the load at a speed slightly less than νc, depending on the velocity factor. If ZL = Z0, the load absorbs all the power, and none is reflected. The only waves then present are the voltage and current (in phase) traveling waves from generator to load.
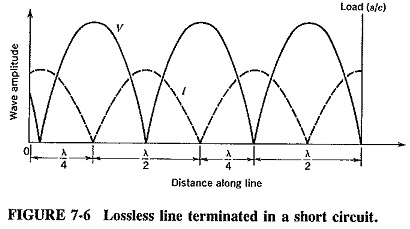
If ZL is not equal to Z0, some power is absorbed, and the rest is reflected. We thus have one set of waves, V and I, traveling toward the load, and the reflected set traveling back to the generator. These two sets of traveling waves, going in opposite directions (180° out of phase), set up an interference pattern known as Standing Waves in Transmission Lines, i.e., beats, along the line. This is shown in Figure 7-6 for a short-circuited line. It is seen that stationary voltage and current minima (nodes) and maxima (antinodes) have appeared. They are separated by half the wavelength of the signal. Note that voltage nodes and current antinodes coincide on the line, as do current nodes and voltage antinodes.
Consider only the forward traveling voltage and current waves for the moment. At the load, the voltage will be zero and the current a maximum because the load is a short circuit. Note that the current has a finite value since the line has an impedance. At that instant of time, the same conditions also apply at a point exactly one wavelength on the generator side of the load, and so on. The current at the load is always a maximum, although the size of this maximum varies periodically with time, since the applied wave is sinusoidal.
The reflection that takes place at the short circuit affects both voltage and current. The current now starts traveling back to the generator, unchanged in phase (series circuit theory), but the voltage is reflected with a 180° phase reversal. At a point exactly a quarter-wavelength from the load, the current is permanently zero (as shown in Figure 7-6). This is because the forward and reflected current waves are exactly 180° out of phase, as the reflected wave has had to travel a distance of λ/4 + λ/4 = λ/2 farther than the forward wave. The two cancel, and a current node is established. The voltage wave has also had to travel an extra distance of λ/2, but since it underwent a 180° phase reversal on reflection, its total phase change is 360°. Reinforcement will take place, resulting in a voltage antinode at precisely the same point as the current node.
A half-wavelength from the load is a point at which there will be a voltage zero and a current maximum. This arises because the forward and reverse current waves are now in phase (current has had to travel a total distance of one wavelength to return to this point). Simultaneously the voltage waves will cancel, because the 180° phase reversal on reflection must be added to the extra distance the reflected wave has to travel. All these conditions will repeat at half-wavelength distances, as shown in Figure 7-6. Every time a point is considered that is λ/2 farther from the load than some previously considered point, the reflected wave has had to travel one whole wavelength farther. Therefore it has the same relation to the forward wave as it had at the first point.
It must be emphasized that this situation is permanent for any given load and is determined by it; such waves are truly Standing Waves in Transmission Lines. All the nodes are permanently fixed, and the positions of all antinodes are constant. Many of the same conditions apply if the load is an open circuit, except that the first current minimum (and voltage maximum) is now at the load, instead of a quarter-wavelength away from it. Since the load determines the position of the first current node, the type of load may be deduced from the knowledge of this position.
Standing Wave Ratio (SWR):
The ratio of maximum current to minimum current along a transmission line is called the standing wave ratio, as is the ratio of maximum to minimum voltage, which is equal to the current ratio.
The SWR is a measure of the mismatch between the load and the line, and is the first and most important quantity calculated for a particular load. The SWR is equal to unity (a desirable condition) when the load is perfectly matched. When the line is terminated in a purely resistive load, the standing wave ratio is given by
where
RL is the load resistance.
It is customary to put the larger quantity in the numerator of the fraction, so that the ratio will always be greater than 1. Regardless of whether the load resistance is half as large or twice as large as the line characteristic impedance, the ratio of a voltage maximum to a voltage minimum is 2:1, and the degree of mismatch is the same in both cases.
If the load is purely reactive, SWR will be infinity. The same condition will apply for a short-circuit or an open-circuit termination. Since in all three cases no power is absorbed, the reflected wave has the same size as the forward wave. Somewhere along the line complete cancellation will occur, giving a voltage zero, and hence SWR must be infinite. When the load is complex, SWR can still be computed, but it is much easier to determine it from a transmission-line calculator, or to measure it.
The higher the SWR, the greater the mismatch between line and load or, for that matter, between generator and line. In practical lines, power loss increases with SWR, and so a low value of standing wave ratio is always sought, except when the transmission line is being used as a pure reactance or as a tuned circuit.
Normalization of impedance:
It is customary to normalize an impedance with respect to the line to which it is connected, i.e., to divide this impedance by the characteristic impedance of the line, as
thus obtaining the normalized impedance. (Note that the normalized impedance is a dimensionless quantity, not to be measured or given in ohms.) This is very useful because the behavior of the line depends not on the absolute magnitude of the load impedance, but on its value relative to Z0. This fact can be seen from Equation (7-8); the SWR on a line will be 2 regardless of whether Z0 = 75 Ω and RL = 150 Ω or Z0 = 300 Ω and RL = 600 Ω. The normalizing of impedance opens up possibilities for transmission-line charts. It is similar to the process used to obtain the universal response curves for tuned circuits and RC-coupled amplifiers.
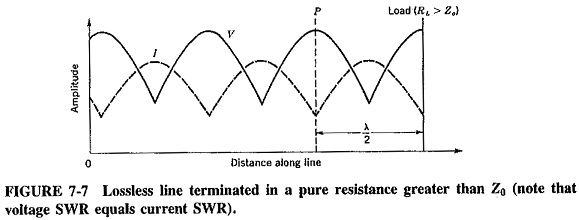
Consider a pure resistance connected to a transmission line, such that RL ≠ 4. Since the voltage and current vary along the line, as shown in Figure 7-7, so will the resistance or impedance. However, conditions do repeat every half-wavelength, as already outlined. The impedance at P will be equal to that of the load, if P is a half-wavelength away from the load and the line is lossless.