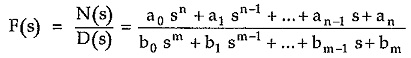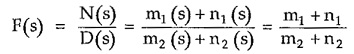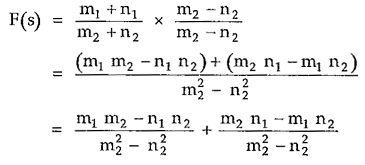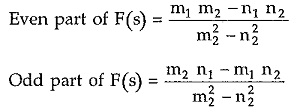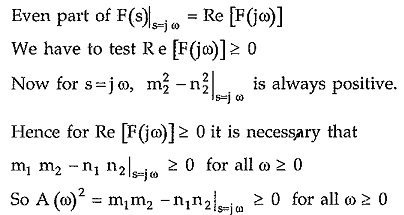Positive Real Function:

Let us study another class of functions called positive real functions. The significance of positive real functions is that if the driving point immitance (i.e. admittance or impedance) is a positive real function then only it is physically realizable using passive R, L and C components. Hence immitance function must be checked for positive realness before synthesizing.

For a function to be positive real function it has to satisfy the following basic properties,

• The given function F(s) is real for real s.

• The real part of F(s) is greater than or equal to zero, when the real part of s is greater than or equal to zero.

• The function F(s) is rational function.

The positive real function is also called Brune function. In addition to the basic properties, the positive real function has some more properties.

Properties of Positive Real Function:

Let

The function F(s) is positive real function having following properties,

1. The coefficients of the numerator and denominator polynomials N(s) and D(s) in F(s) are real and positive.

Hence,

• F(s) is real when s is real.
• The complex poles and zeros of F(s) occur in complex conjugate pairs.
• The scale factor, N = N = a₀/b₀ is real and positive.

2. The poles and zeros of F(s) are having negative or zero real parts.

3. The poles of F(s) on the imaginary (jω) axis must be simple. Their residues must be real and positive. The same statement is true for the poles of 1/F(s).

4. The degrees of the numerator and denominator polynomials in F(s) differ at the most by 1. So degrees m and n must differ at the most by 1. Thus the number of finite poles and finite zeros of F(s) differ at the most by 1.

5. The terms of lowest degree in the numerator and denominator polynomials of F(s) differ in degree at most by 1. So F(s) has neither multiple poles nor zeros at the origin.

6. If F(s) is positive real function then 1/F(s) is also positive real function. Thus for a network if driving point impedance function Z(s) is positive real then the driving point admittance function Y(s) = 1/Z(s) is also positive real.

7. The sum of positive real functions is also positive real. If two impedances are in series, the sum of the impedances is positive real. Similarly if two admittances are in parallel, their addition gives positive real admittance. Note that the difference in two positive real functions is not necessarily a positive real function.

These properties are nothing but necessary conditions for the given function to be positive real but are not sufficient conditions.

Procedure for Testing a Function for Positive Realness:

Let F(s) be the function to be tested for the positive realness, which is a ratio of two polynomials N(s) and D(s). Remove all the common factors in the numerator and the denominator before testing for the positive realness.

The testing procedure can be divided as,

1. Testing for necessary conditions
2. Testing for necessary and sufficient conditions

Inspection Test for Necessary Conditions:

By inspecting the given function, the following requirements are tested,

1. All the coefficients of different polynomials must be real and positive.
2. The degrees of numerator and denominator polynomials differ at most by 1.
3. Lowest degree in numerator and denominator differ at most by 1.
4. The imaginary axis poles and zeros of F(s) must be simple in nature. No multiple pole or zero should lie on the imaginary axis.
5. There should be no missing terms in numerator and denominator unless all even or all odd terms are missing.
6. The poles and zeros of F(s) must be located in the left half of s-plane.
7. There should not be multiple poles or zeros either at origin (s = 0) and/or at infinity (s = ∞).
8. The simple poles on jω axis should have real and positive residues.

Test for Necessary and Sufficient Conditions:

The tests for necessary and sufficient conditions are,

1. The function F(s) must be real when s is real.

2. If F(s) = N(s)/D(s)

then N(s) + D(s) must be Hurwitz.

For N(s) + D(s) to be Hurwitz, all the quotients obtained by expressing it in continued fraction expansion must be positive. Also the continued fraction expansion should not terminate abruptly.

3. Re [F(jω)] ≥ 0 for all ω.

The real part of F (jω) must be greater than equal to zero for all ω.

To test this, separate the numerator and denominator polynomials into even and odd parts.

Multiply numerator and denominator by m₂ – n₂

It is known that,

• Product of two even functions is an even function.
• Product of two odd functions is an even function.
• Product of an odd function and an even function is an odd function.

So as m₁ and m₂ are even, m₁ m₂ is even.

And n₁ and n₂ are odd, n₁ n₂ is even.

Also m₁ n₂ and m₂ n₁ is odd as the product of even and odd function.

Finally m²₂ and n²₂ are both even.

Hence in the above equation of F(s), first part is even while the second part is odd.

Hence substituting s =jω in the even part gives the real part of F(jω) while substituting s =jω in odd part gives imaginary part of F(s).

In most of the cases, the condition can be verified by factorising A (ω²). If factorization is not sufficient for the required conclusion then A (ω²) is plotted over sufficiently large range of ω and it is ensured that it is not negative.

Thus the testing procedure for positive realness of a function can be summarized as,

1. Check all the necessary conditions by inspection.

2. For all the poles and zeros of F(s) to be in the left half of s-plane or on the imaginary axis, N(s) and D(s) polynomials must be Hurwitz.

3. If F(s) has poles on imaginary axis, the residues at the poles must be real and positive.

Find the partial fractions of F(s) where s = ± jω₀ is the pair of poles on imaginary axis.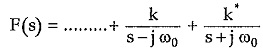

So coefficients k and k^· which are complex conjugates of each other must be real and positive.

4. Finally test that

This can be done by factorising A (ω²). This also can be tested by plotting A (ω²) graph against ω² or using Sturm’s theorem.