Modes of Operation of Electrical Drive:

Three types of Modes of Operation of Electrical Drive:

• Steady-State

• Acceleration including starting

• Deceleration including stopping

As we know already, steady-state operation takes place when motor torque equals the load torque. The steady-state operation for a given speed is realized by the adjustment of steady-state motor speed-torque curve such that the motor and load torques are equal at this speed. Change in speed is achieved by varying the steady-state motor speed torque curve so that motor torque equals the load torque at the new desired speed.

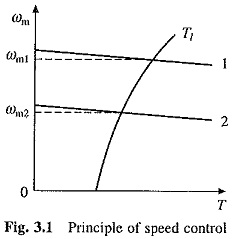
In Fig. 3.1 when the motor parameters are adjusted to provide speed torque curve 1, drive runs at the desired speed ω_m1. Speed is changed to ω_m2 when the motor parameters are adjusted to provide speed-torque curve 2. When load torque opposes motion, the motor works as a motor operating in quadrant.I or III depending on the direction of rotation. When the load is active it can reverse its sign and act to assist the motion. For example, when a loaded hoist is lowered or an unloaded hoist is lifted, the net load-torque acts to assist the motion. Steady-state operation for such a case can be obtained by adding a mechanical brake which will produce a torque in a direction to oppose the motion. The steady state operation is obtained at a speed for which braking torque equals the load torque. Drive operates in quadrant II or IV depending on the direction of rotation. Mechanical braking has a number of  disadvantages: frequent maintenance and replacement of brake shoes, lower life, braking power is always wasted as heat. These disadvantages are overcome by the use of electrical braking in which the motor is made to work as a generator converting mechanical energy to electrical energy and producing torque in a direction so as to oppose the motion. Even when electrical braking is employed, the mechanical brakes may also be provided to ensure reliable operation of the drive. Mechanical brakes are also employed to hold the drive at standstill because many braking methods are not able to produce torque at stand-still.

Acceleration and deceleration modes are transient operations. Drive operates in acceleration mode whenever an increase in its speed is required. For this motor speed-torque curve must be changed so that motor torque exceeds the load torque. Time taken for a given change in speed depends on inertia of motor-load system and the amount by which motor torque exceeds the load torque.

Increase in motor torque is accompanied by an increase in motor current. Care must be taken to restrict the motor current within a value which is safe for both motor and power modulator. In applications involving acceleration periods of long duration, current must not be allowed to exceed the rated value. When acceleration periods are of short duration a current higher than the rated value is allowed during acceleration. In closed-loop drives requiring fast response, motor current may be intentionally forced to the maximum value in order to achieve high acceleration. Torque developed by an ac motor for a given current is usually a function of motor control method employed. In high performance drives, methods which produce high torque per ampere of motor current, are employed.

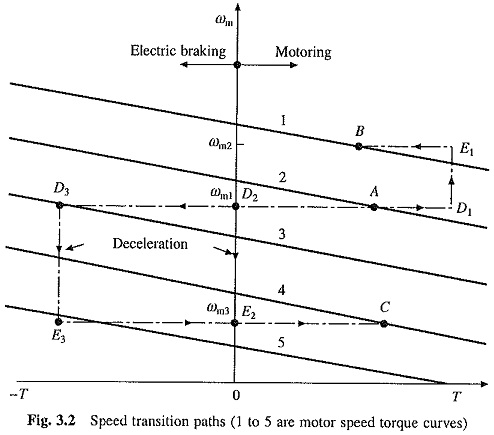
Figure 3.2 shows the transition from operating point A at speed ω_m1 to operating point B at a higher speed ω_m2, when the motor torque is held constant during acceleration. The path consists of AD₁E₁B. In Fig. 3.2, 1 to 5 are motor speed-torque curves. Starting is a special case of acceleration where a speed change from 0 to a desired speed takes place. All points mentioned in relation to acceleration are applicable to starting. The maximum current allowed should not only be safe for motor and power modulator but the drop in source voltage caused due to it should also be in acceptable limits. For each motor, a number of methods are available for limiting the starting current. In ac motors, the starting torque per ampere has different values for different starting methods. When starting takes place at no load or light loads, the methods with low starting torque can be employed. When the motor must start with substantial load torque (around rated torque) or when fast start is required, methods with high starting torque must be used. In some applications the motor should accelerate smoothly, without any jerk. This is achieved when the starting torque can be increased steplessly from its zero value. Such a start is known as Soft Start.

Modes of Operation of Electrical Drive in deceleration mode is required when a decrease in its speed is required. As we know, deceleration occurs when load torque exceeds the motor torque. In those applications where load torque is always present with substantial magnitude, enough deceleration can be achieved by simply reducing the motor torque to zero. In those applications where load torque may not always have substantial amount or where simply reducing the motor torque to zero does not provide enough deceleration, mechanical brakes may be used to produce the required magnitude of deceleration. Alternatively, electric braking may be employed. Now both motor and the load torque oppose the motion, thus producing larger deceleration.

During electric braking motor current tends to exceed the safe limit. Appropriate changes are made to ensure that the current is restricted within safe limit. When electric braking may persist for long periods, maximum current is usually restricted to the rated value. When electric braking occurs for short duration, maximum current is allowed to exceed the rated value. Higher the braking torque greater is the deceleration. Therefore, in high performance closed loop schemes, motor current may be intentionally forced to the maximum permissible value during deceleration. Figure 3.2 shows paths followed during transition from point A at speed ω_m1 to a point Cat a lower speed ω_m3. When deceleration is carried out using electric braking at a constant braking torque, the operating point moves along the path AD₃E₃C. When sufficient load torque is present or when mechanical braking is used the Modes of Operation of Electrical Drive takes place along the path AD₂E₂C. Stopping is a special case of deceleration where the speed of a running motor is changed to zero. All the discussions about deceleration are applicable to stopping also. In applications requiring frequent, quick, accurate or rapid emergency stops, the electric braking is usually employed. It allows smooth and quick stops without subjecting the mechanical parts to unduly large stresses, e.g. in suburban electric trains quick stops are required. Use of electric braking allows a smooth stop which does not cause any inconvenience to passengers and increases the life of track and wheels allowing a substantial saving in cost.