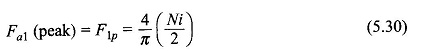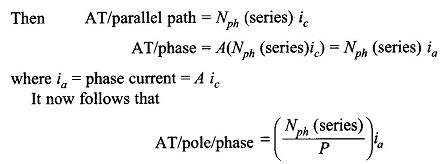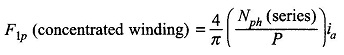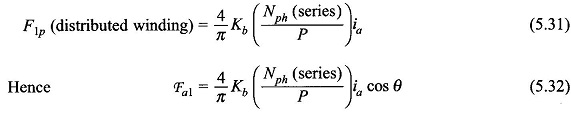MMF of AC Distributed Winding:
It has been seen earlier that the armature what-when-how.comof a practical machine has distributed winding wound for the same number of poles as the field winding. As the armature carries current, the resultant field of its current-carrying coils has the same number of poles as the field winding. Our approach will be to find the MMF of AC Distributed Winding of the current-carrying armature by superimposing the mmf space waves of individual coils.
MMF Space Wave of a Single Coil:
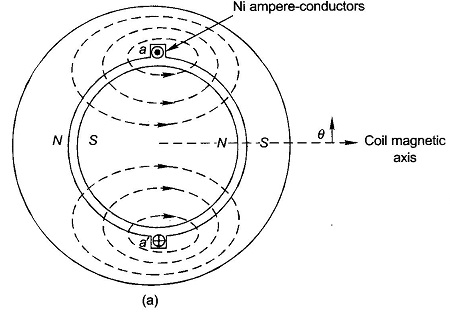
A cylindrical rotor machine with small air-gap as shown in Fig. 5.24(a) will be assumed here. The stator is imagined to be wound for two-poles with a single N-turn full-pitch coil carrying current i in the direction indicated. The figure shows some flux lines of the magnetic field set up. A north and corresponding south pole are induced on the stator periphery. The magnetic axis of the coil is from the stator north to the stator south. Each flux line radially crosses the air-gap twice, normal to the stator and rotor iron surfaces and is associated with constant mmf Ni. On the assumption that the reluctance of the iron path is negligible, half the mmf (Ni/2) is consumed to create flux from the rotor to stator in the air-gap and the other half is used up to establish flux from the stator to rotor in the air-gap. Mmf and flux radially outwards from the rotor to the stator (south pole on stator) will be assumed to be positive and that from the stator to rotor as negative.
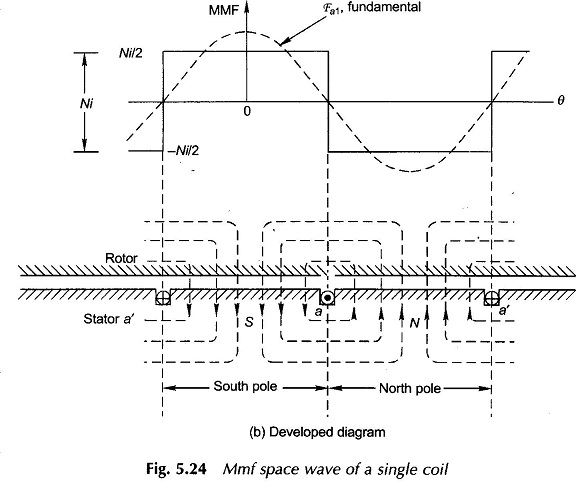
The physical picture is more easily visualized by the developed diagram of Fig. 5.24(b) where the stator with the winding is laid down flat with the rotor on the top of it. It is seen that the mmf is a rectangular space wave wherein mmf of + Ni/2 is consumed in setting flux from the rotor to stator and mmf of – Ni/2 is consumed in setting up flux from the stator to the rotor. It has been imagined here that the coil-sides occupy a narrow space on the stator and the mmf changes abruptly from – Ni/2 to + Ni/2 at one slot and in reverse direction at the other slot. The mmf change at any slot is
and its sign depends upon the current direction.
The mmf space wave of a single coil being rectangular, it can be split up into its fundamental and harmonics. It easily follows from the Fourier series analysis that the fundamental of the mmf wave as shown in Fig. 5.24(b) is
where θ is the electrical angle measured from the magnetic axis of the coil which coincides with the positive peak of the fundamental wave.
From now onwards only the fundamental mmf wave of a current-carrying coil will be considered, neglecting its associated harmonic space waves whose amplitudes are small. Furthermore, as will soon be seen, in a MMF of AC Distributed Winding, the rectangular mmf waves of individual phase group coils add up to produce a mmf wave closer to a sine wave, i.e. the harmonics tend to cancel out.
It may be noted here that with the assumption of the narrow air-gap, the mmf distribution will be the same if the coils were located in the rotor slots instead.
MMF Space Wave of One Phase of a Distributed Winding:
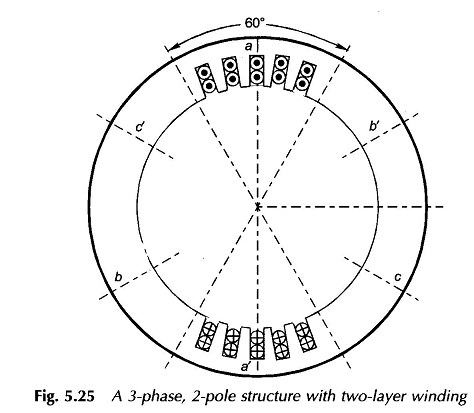
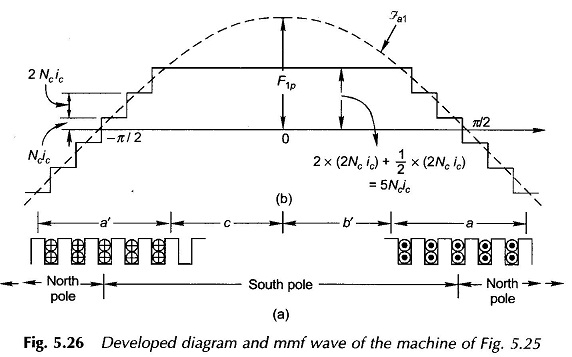
Consider now a basic 2-pole structure with a round rotor, with 5 slots/pole/phase (SPP) and a 2-layer winding as shown in Fig. 5.25. The corresponding developed diagram is shown in Fig. 5.26(a) along with the mmf diagram which now is a stepped wave obviously closer to a sine wave than the rectangular mmf wave of a single coil (Fig. 5.24(b)). Here since SPP is odd (5), half the ampere-conductors of the middle slot of the phase group a and a′ contribute towards establishment of south pole and half towards north pole on the stator. At each slot the mmf wave has a step jump of 2Ncic, ampere-conductors where Nc = coil turns (equal to conductors/layer) and ic = conductor current.
Now F1p, the peak of the fundamental of the mmf wave, has to be determined. Rather than directly finding the fundamental of the stepped wave, one can proceed by adding the fundamentals of the mmf s of individual slot-pairs (with a span of one pole-pitch). These fundamentals are progressively out of phase (space phase as different from time phase) with each other by the slot angle γ. This addition is easily accomplished by defining the breadth factor Kb, which will be the same as in the case of the generated emf of a coil group.
Let
provided the winding is a concentrated one. The fundamental peak of the concentrated winding is then
Since the actual winding is a distributed one, the fundamental peak will be reduced by a factor Kb. Thus
where the pole axis is taken as the angle reference (Fig. 5.26(b)).
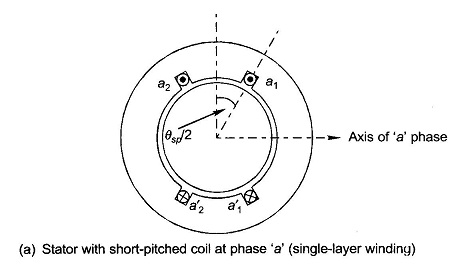
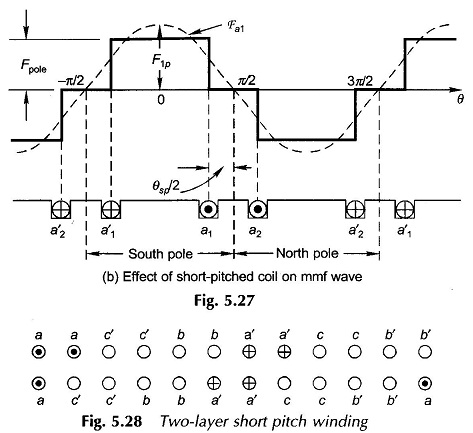
The effect on the mmf wave of short-pitched coils can be visualized by Fig. 5.27 in which the stator has two short-pitched coils (a1a′1, a2a′2) for phase a of a 2-pole structure. The mmf of each coil establishes one pole. From the developed diagram of Fig. 5.27(b) it is seen that the mmf wave is rectangular but of shorter space length than a pole-pitch. The amplitude of the fundamental peak gets reduced by a factor Kp, called the pitch factor, compared to the full-pitch rectangular mmf wave. It can be shown by Fourier analysis that
It is not surprising that the same result is obtained for Kp for the space mmf wave as for the generated emf in a short-pitched coil.
In general when the MMF of AC Distributed Winding and short-pitched, the fundamental space mmf of phase a as in Eq. (5.32) generalizes to
Like in the case of the induced emf, MMF of AC Distributed Winding of stator winding and short-pitching both help in reducing harmonics in the space mmf wave. In the analysis from now onwards, it will be assumed that the space mmf wave created by each phase of the stator winding when carrying current is purely sinusoidal. Also Kb and Kp are defined in the same manner as for the induced emf.
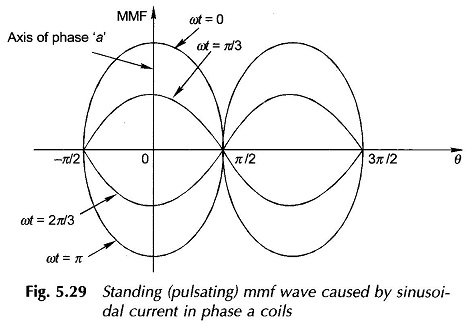
When the phase a carries sinusoidal current
As per Eq. (5.36), the mmf of one phase is a standing wave (pulsating wave) in space whose peak always coincides with the phase axis while the peak amplitude varies sinusoidally with time. This is illustrated in Fig. 5.29, where a half-cycle of pulsation is indicated.