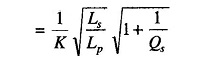Measurements of very Large Currents by Thermocouples:

Measurements of very Large Currents by Thermocouples – Thermocouples instruments with heaters large enough to carry very large currents may have an excessive skin effect. Ordinary shunts cannot be used because the shunting ratio will be affected by the relative inductance and resistance, resulting in a frequency effect.

One solution to this problem consists of minimizing the skin effect by employing a heater, which is a tube of large diameter, but with very thin walls.

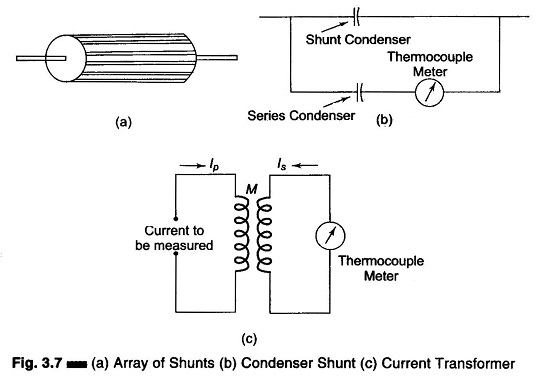
Another consists of employing an array of shunts of identical resistance arranged symmetrically as shown in Fig. 3.7 (a).

In. Fig. 3.7 (a) each filament of wire has the same inductance, so that the inductance causes the current to divide at high frequencies, in the same way as does the resistance at low frequencies. In Fig. 3.7 (b) the condensor shunt is used such that the current divides between the two parallel capacitors proportional to their capacitance, and maintains this ratio independent of frequency, as long as the capacitor that is in series with the thermocouple has a higher impedance than the thermocouple heater and the lead inductance is inversely proportional to the capacitances.

In Fig. 3.7 (c) the current transformer is used to measure very large RF currents at low and moderate frequencies using a thermocouple instrument of ordinary range. Such transformers generally use a magnetic dust core. The current ratio is given by Primary Current/Secondary Current

where

• L_s = secondary inductance
• L_p = primary inductance
• K = coefficient of coupling between L_p and L_s
• r_{s =} resistance of secondary, including meter resistance
• Q_s = ωL_s/r_s = Q of the secondary circuit taking into account meter resistance

If Q of the secondary winding is appreciable (i.e. greater than 5), the trans­formation ratio is independent of frequency.

A current ratio of 1000 or more can be obtained at low and moderate RF by using a many turn secondary wound on a toroidal ring.