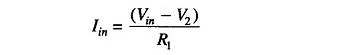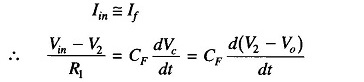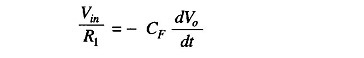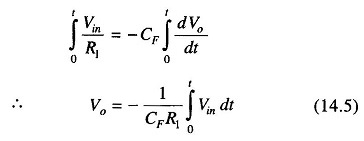Integrator using Op Amp:

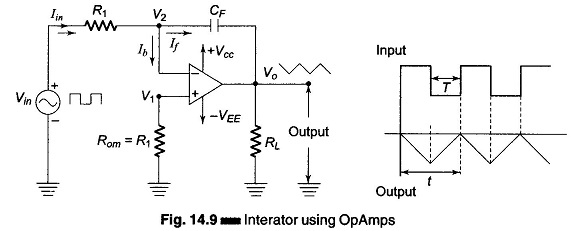
An Integrator is a circuit that performs the mathematical operation of integra­tion because it produces an output voltage that is proportional to the integral of the input. The Integrator using Op Amp is shown in Fig. 14.9.

A common application is to use a constant input voltage to produce a ramp voltage. (A ramp voltage is a linearly increasing or decreasing voltage.) The typical input to the integrator is a rectangular pulse. V_in is the constant input voltage of time T applied to the inverting terminal. Because negligible current flows into the opamp, the input current is constant and equals I_in = V_in/R₁. Approximately all the current goes to the capacitor C_F. As C = Q/V or V = Q/C and since a constant current is flowing into the capacitor, the charge Q increases linearly. This means that the capacitor voltage increases linearly. Because of the phase reversal of the opamp, the output voltage is a negative ramp. At the negative pulse period of the input signal, the direction of the charging current is opposite, hence the output is an increasing ramp.

An integrator circuit is obtained by using a basic inverting amplifier configu­ration and by replacing the feedback resistor R_F by a capacitor C_F. The expres­sion for the output voltage V_o can be obtained by using Kirchhoff’s current equation.

I_in = I_f + I_b, since I_b is negligible, I_in ≡ I_f. The current through the capacitor is given by

But

As

But

Therefore

The output voltage can be obtained by integrating both sides with respect to time, hence

This equation says that the output voltage is directly proportional to the negative integral of the input voltage and inversely proportional to the time constant C_F R₁.

The input impedance of the Integrator using Op Amp circuit is equal to the resistance R₁, the output impedance is low because of the negative feedback which is inherent in the circuit. CR is called the time constant of the integrator. For perfect integration, the time period T of the input signal must be longer than or equal to the time constant C_F R₁. In order to minimize the offset voltages, a resistor R_om called the “offset minimize resistor” is connected to the non-inverting terminal of the op-amp.

The integral of a sine function is a cosine function, hence, if a sine wave input is applied to an integrator, the output is a cosine wave. Also, if a square wave input is applied, the output is a triangular wave.

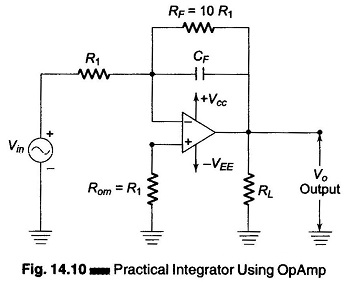
A practical Integrator using Op Amp is shown in Fig. 14.10.

At low frequency and dc signals, the capacitor acts like an open circuit. Hence the closed loop voltage gain equals the open loop voltage gain. This produce too much output offset voltage. At zero frequency (DC) and without negative feedback, the circuit treats the input offsets as an valid input signal charges the capacitor. This drives the output into positive or negative saturation.

Hence a way to minimize the effect of these input offsets is to roll off the voltage gain at low frequencies by inserting a resistor R_F in parallel with the capacitor, as shown in Fig. 14.10. The resistor used should be at least 10 times greater than the input resistance.

The integrator is most commonly used in analog computer, A/D conversion and signal wave shaping.