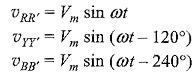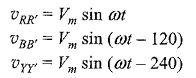Generation of Three Phase Voltage:
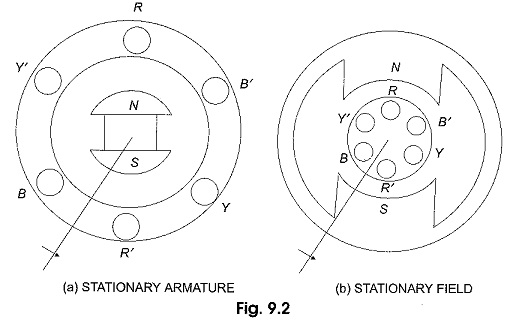
Three Phase Voltage can be generated in a stationary armature with a rotating field structure, or in a rotating armature with a stationary field as shown in Fig. 9.2 (a and b).
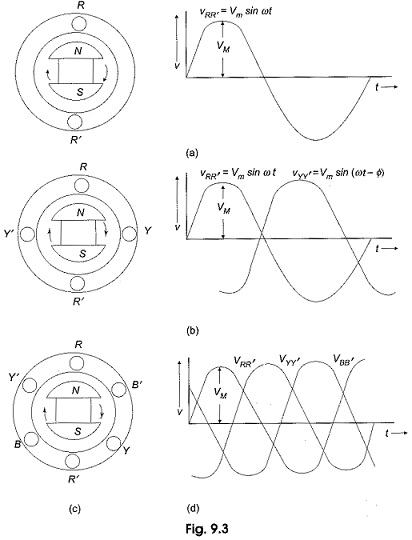
Single phase voltages and currents are generated by single phase generators as shown in Fig. 9.2(a). The armature (here a stationary armature) of such a generator has only one winding, or one set of coils. In a two-phase generator the armature has two distinct windings, or two sets of coils that are displaced 90° (electrical degrees) apart, so that the generated voltages in the two phases have 90 degrees phase displacement as shown in Fig. 9.3(b).
Similarly, Three Phase Voltage are generated in three separate but identical sets of windings or coils that are displaced by 120 electrical degrees in the armature, so that the voltages generated in them are 120° apart in time phase. This arrangement is shown in Fig. 9.3(c). Here RR’ constitutes one coil (R-phase); YY’ another coil (Y-phase), and BB’ constitutes the third phase (B-phase). The field magnets are assumed in clockwise rotation.
The voltages generated by a three-phase alternator is shown in Fig. 9.3(d). The Three Phase Voltage are of the same magnitude and frequency; but are displaced from one another by 120°. Assuming the voltages to be sinusoidal, we can write the equations for the instantaneous values of the voltages of the three phases. Counting the time from the instant when the voltage in phase R is zero. The equations are
At any given instant, the algebraic sum of the three voltages must be zero.
Phase Sequence:
Here the sequence of voltages in the three phases are in the order υRR′ – υYY′ – υBB′, and they undergo changes one after the other in the above mentioned order. This is called the phase sequence. It can be observed that this sequence depends on the rotation of the field. If the field system is rotated in the anticlockwise direction, then the sequence of the voltages in the three-phases are in the order υRR′ – υBB′ – υYY′,; briefly we say that the sequence is RBY. Now the equations can be written as