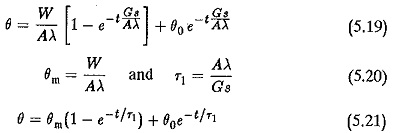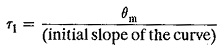Electric Motor Cooling and Heating:
The geometry of an Electric Motor Cooling is too complex to predict accurately the heat flow and temperature distribution. This is a difficult task. A portion of the conductors of armature winding are embedded in slots and some portion is outside the iron material as overhang. The heating calculations are also complicated by the loading of the motor. The direction of heat flow does not remain the same at all loaded conditions. At no-load or lightly loaded conditions heat flows from iron parts to the winding due to the temperature gradient. When once the load increases the gradient changes as the heat (loss) generated in the winding is greater than the heat(loss) generated in iron and consequently heat flows from the winding to iron core. A considerable simplification is therefore necessary to compute the temperature rise of a motor.
The heating and Electric Motor Cooling calculation are based on the following simplifications:
1.The machine is considered to be a homogeneous body having a uniform temperature gradient. All the points at which the heat is generated have the same temperature. All the points at which the heat is dissipated to the cooling medium are also at the same temperature.
2.Heat dissipation taking place is proportional to the difference of temperatures of the body and surrounding medium. No heat is radiated.
3.The rate of dissipation of heat is constant at all temperatures.
Under these assumptions a machine develops heat internally at a uniform rate and gives it to the surroundings proportional to the temperature rise. It can be shown that the temperature rise of a body follows an exponential law. Assuming the heat developed is proportional to the losses, we have the heat balance equation.
where
W – is the power loss on the motor responsible for heat, Watts.
G – weight of active parts of the motor in kg
s – specific heat of the material of the body in J/degree/kg
A – cooling surface in m2
λ – specific heat dissipation or emissivity in J/s/m2/degree difference in temperature
θ – is temperature rise of the body
dθ – temperature rise in a small interval dt
Equation (5.2) indicates that the total heat generated in the body (W dt) is equal to the sum of the heat dissipated to the surrounding medium (Aλθ dt) and the heat stored in the body causing a temperature rise θ above the ambient (Gs dθ).
The following results may be obtained by a close examination of Eq. 5.2.
When the temperature rise reaches a constant value, the body is said to have reached maximum temperature rise θm. When this condition is reached dθ = 0. The heat developed in the body is completely dissipated to the surroundings. No more heat is stored in the body and the body attains thermal equilibrium. Therefore,
and the maximum temperature rise
Rearranging Eq. 5.2 we have
If the Electric Motor Cooling were not there the machine would heat up enormously and the temperature rise would attain very high values. But θ must be limited to θm. The time taken by the machine to reach this temperature rise in the absence of dissipation can be determined using
which gives a linear relation between θ and t. Therefore
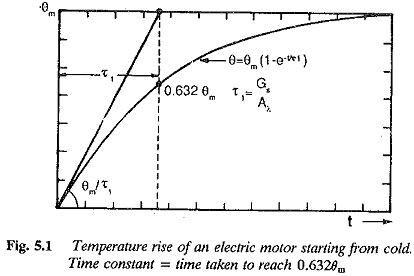
If r1 is the time taken to reach θm (Fig. 5.1). We have
Substituting for θm from Eq. 5.4 we have the value of r1, the time taken by the body to reach the maximum temperature rise
r1 is called the thermal (heating) time constant. In other words this happens to be the time taken by the motor to reach the final steady-state temperature rise if the initial rate of rise of temperature continues.
Heat balance equation (Eq. 5.2) must be solved to obtain a relationship between the temperature rise and time. Rearranging Eq. 5.2 we have
from which
Integrating both sides we have
where log C1 is a constant of integration. It is evaluated using the initial conditions at the start of heating. This equation can be written as
For simplicity, it is assumed that the machine is started from cold. Therefore θ = 0, at t = 0.
Substituting for C1 and rearranging the terms we have
Using relations of Eqs 5.8 and 5.9 we have
Figure 5.1 depicts the temperature rise curve.
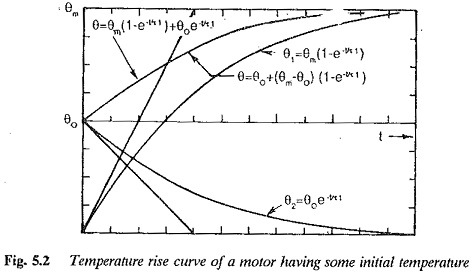
However while considering the heating and Electric Motor Cooling, in many cases the initial temperature rise is not zero, i.e., at t = 0, θ = θ0.
Substituting the initial conditions in Eq. 15.12 we have
Using the value of C1 in Eq. 5.13.
Rearranging the terms we get
The heating curve can be looked upon (Fig. 5.2) as the sum of two curves:
1.heating curve when the machine has a load to give a maximum temperature rise of θm.
2.cooling curve when the machine is disconnected from supply with an initial temperature rise of θ0.
Heating time constant r1 : r1 in Eqs 5.16 and 5.21 is called the heating time constant. It can be seen from Eq. 5.5 that it would have been the time taken by the ineffective or had the initial rate of rise of temperature been continued, i.e,
But the machine has cooling, machine takes longer time to reach the maximum temperature rise and the time is greater than r1 Substituting t = r1 in equation we see that the temperature rise of the body is 63.2% of θm. Therefore it can be defined as the time taken by the machine to reach a temperature rise of 63.2% of maximum temperature rise. These are all depicted in Fig. 5.1,
The value of r1 gives an an idea of the effectiveness of cooling. Well ventilated machines have smaller time constants. The time constants of open machines are of the order of 25 minutes. The totally enclosed machines have poor ventilation.
Heating time constant can be determined from the experimental curve using the definition that it is the time taken to reach the 63.2% of θm. The The time constant
Cooling curve
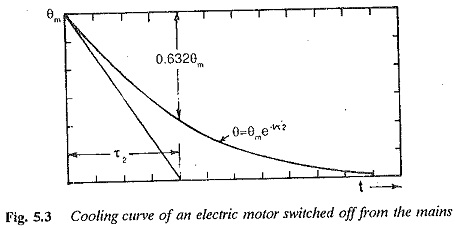
When a machine is switched off from the mains or when the load on the motor is reduced, the machine cools. In the first case it cools to the ambient temperature and in the second case it cools to a temperature determined by the power losses at reduced load. The cooling curve is also an exponential curve. When the machine is switched off there is no heat generation in the motor and all the heat stored in the machine is now dissipated to the surroundings. In this Eq. 5.2 reduces to
Where r2 is the time constant during cooling. Fig. 5.3 depicts the curve.
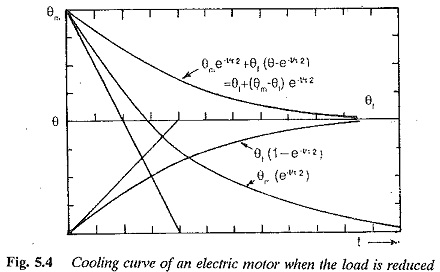
The machine sometimes is not switched off but load on it is reduced in which case it cools to a temperature
where W1 is the total loss at reduced load. The cooling curve in this case determined as
which can also be written as
The cooling curve is shown in Fig. 5.4. This may also be looked upon as the sum of two curves
1.heating curve as if the machine is loaded to give a maximum temperature rise of θf.
2.cooling curve as if the machine is disconnected from the supply when it had a temperature rise of θm.
r2 in the cooling curve is the cooling time constant. The heating time constant r1 and cooling time constant r2 are not equal in self cooled machines. r2 is two to three times greater than r1. All other conditions being equal, the time taken by the motor to cool to ambient temperature is longer than the time taken by the motor for heating. If forced cooling is employed r2 = r1. In such cases the heating curve and cooling curve are mirror images of each other.
The power rating of a motor for a particular operating condition is selected based on the thermal rating of the motor, so that it meets the specification regarding the final steady-state temperature rise, i.e., it must be equal to or slightly less than the permissible temperature rise.
As has already been pointed out, an Electric Motor Cooling has a very good overload capacity. The Duration of overload is normally till the motor reaches the permissible temperature rise. This overload must be within pull-out torque capability of the motor.
A motor can therefore be selected for a given class of duty based on its thermal rating with due consideration to pull-out torque capability.