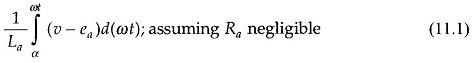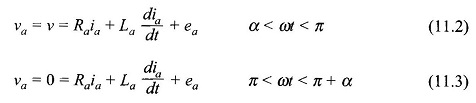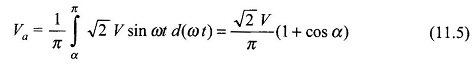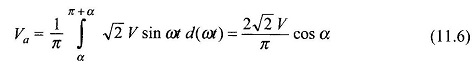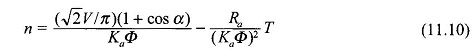DC Motor Control through Converters:
DC motor control is conveniently and efficiently achieved by phase-controlled converters wherein the ac input voltage is converted to a controlled dc output. The commutation process, the transfer of current from one thyristor to the other, in these converters is the inexpensive natural or line commutation. As, an incoming thyristor is turned-on, it reverse-biases the outgoing thyristor, turning it off. No additional commutation circuitry is therefore required. The power conversion efficiency in these converters is above 95% because of relatively low losses in thyristors. These converters are used in the speed control of fractional-kW dc motors as well as in large motors employed in variable-speed reversing drives for rolling mills with motor ratings as large as several MWs.
In certain types of converters (semi-converters) a diode known as a, free-wheeling diode is connected across motor terminals to allow for dissipation of energy stored in motor inductance and to provide for continuity of motor current when the thyristors are blocked. It also provides protection against transient overvoltages.
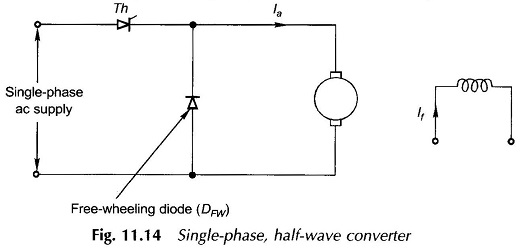
Single Phase Half wave Converter:
Figure 11.14 shows a single-phase half-wave converter for controlling a separately excited DC Motor. It requires a single thyristor and a free-wheeling diode. In this circuit the motor current is always discontinuous, resulting in poor motor performance. This type of converter is employed only for motors below 400 W. It will not be described in detail here; these easily follow from the description of waveforms (voltage and current) for the semi-converter.
Semi-Converter feeding a Separately excited DC Motor:
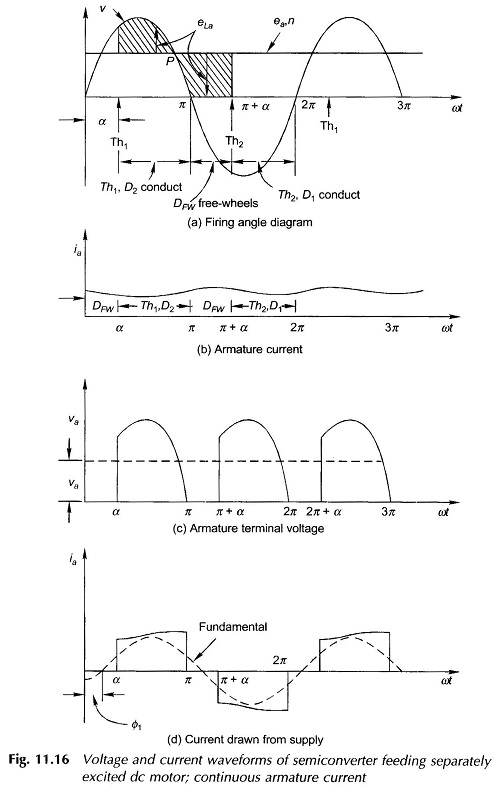
This is a one-quadrant converter (Fig. 11.15a) which gives voltage and current of one polarity at dc terminals. It therefore does not provide for regenerative braking, i.e. power flow from DC Motor Control to the ac supply. Where regeneration is not required, this converter is used for reasons for economy.
Figure 11.15(b) gives the circuitry of a semi-converter feeding a separately excited DC Motor Control. The armature resistance Ra and inductance La are shown lumped in series with an armature-induced emf ea while the armature terminal voltage is va. It has two thyristors, two diodes and a free-wheeling diode (connected across motor terminals). It will be assumed that in steady-state operation the armature current is continuous over the whole range of operation. Typical steady-state voltage and current waveforms are shown in Fig. 11.16. The thyristor Th1 is fired at angle α and Th2 at angle π + α with respect to the supply voltage ν and the process is repeated continuously.
Under steady conditions, as Th1 is fired (ωt = α), Th1 and D2 conduct and the motor is connected to the supply, i.e. νa = ν. At ωt = π, νa tends to become negative as the input voltage polarity changes. This causes DFW, the free-wheeling diode, to become forward-biased and the armature current flowing through Th1D2 is transferred to DFw, which means that Th1 commutates (naturally). The motor terminals are shorted through DFw for the free-wheeling period π < ωt < π + α providing for continuity of the armature current during this period when the motor remains disconnected from the supply. At ωt = π + α, Th2 is fired and Th2D1 conduct, causing DFW to become reverse-biased and therefore open-circuited. The motor is once again connected positively to the supply for the next period of π + α < ωt < 2π. This process repeats continuously.
Various voltage and current waveforms of a separately excited DC Motor Control fed through a semi-converter are shown in Fig. 11.16. Though the voltage across motor terminals (Fig. 11.16(c)) contains harmonics over and above a steady dc value, it is rightly assumed here that the motor does not respond to these harmonics and therefore runs at constant speed (n) and has constant induced emf (ea). As Th1 fires at ωt = α, the motor current is given by
up to the point P shown in Fig. 11.16(a); ν > ea so that the motor current increases. So does the motor emf ea. During this period, apart from the energy being delivered to the load, energy is also being stored in motor inductance (La). Beyond the point P, ν < ea and the motor current begins to decrease. This also implies the reversal of voltage across the motor inductance which now feeds energy into the system. During the free-wheeling period (π < ωt < π + α), the diode continues to be forward-biased by the reversal of the inductive voltage. During this period a part of the energy stored in motor inductance is consumed to feed the mechanical load. The motor current, speed and emf, therefore, all reduce. This process then repeats over the next period (π + α < ωt < 2π + α ) via Th2D1 and later through DFW. The current drawn from the supply shown in Fig. 11.16(d) is that part of the armature current which flows over the periods (α, π), (π + α, 2π), … when the motor is connected to the supply. It is not necessary to use the free-wheeling diode. In its absence at ωt = π, D1 becomes forward-biased so that free-wheeling takes place through Th1D1 till Th2 is fired. At ωt = 2π free-wheeling takes place through Th2D2 and so on.
It should be observed from Fig. 11.16(d) that the fundamental of the current drawn from the mains lags the voltage by an angle Φ1 (< α ).
Discontinuous Armature Current:
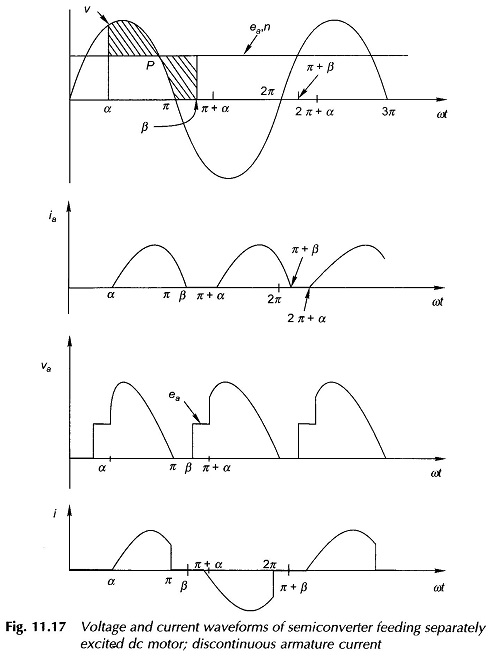
The armature current becomes discontinuous for large values of the firing angle, high speed and low values of torque. The motor performance deteriorates with discontinuous armature current. The ratio of peak to average and rms to average armature current increases. It is, therefore, desirable to operate the motor in the continuous current mode. To achieve this, an external armature circuit choke may be used, which decreases the rate of current decay during the free-wheeling operation.
The voltage and current waveforms for semi-converter with discontinuous current are shown in Fig. 11.17. The motor is connected to supply through Th1D2 for the period α < ωt < π. Beyond π, the motor is shorted through the free-wheeling diode DFW. The armature current decays to zero at angle β (extinction angle) π + α, i.e. before the thyristor Th2 is fired, thereby making the armature current discontinuous. During α to π, the conduction period through Th1D2, the motor terminal voltage is the same as the input voltage. During π to β the motor terminal voltage is zero as motor terminals are shorted by the free-wheeling diode. From β to π + α, the motor coasts and so its terminal voltage is the same as its induced emf.
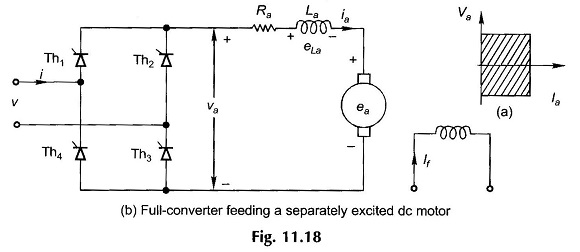
Full-Converter feeding a Separately Excited DC Motor:
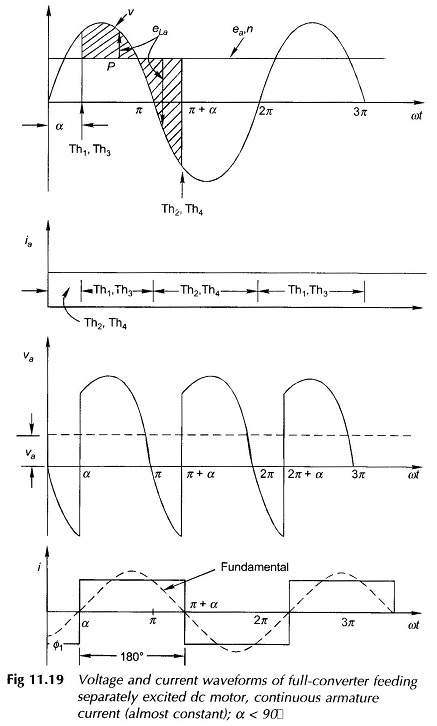
A full-converter is a two-quadrant converter (see Fig. 11.18(a)) in which the voltage polarity of the output can reverse, but the current remains unidirectional because of the unidirectional thyristors. A full-converter employs four thyristors but no free-wheeling diode is required. A full-converter feeding a separately excited DC Motor Control is shown in Fig. 11.18. The voltage and current waveforms are shown in Fig. 11.19 with the assumption that the armature current ia is almost constant. Thyristors Th1 Th3 conduct for the interval α < ωt < π + α and connect the motor to supply. At π + α, thyristors Th2Th4 are triggered. Immediately the supply voltage appears in reverse-bias across Th1 Th3 and turns them off. This is natural or line commutation. The motor current is transferred from Th1 Th3 to Th2Th4. Since there is no period when the motor is disconnected from supply, no free-wheeling is necessary. During α to π , energy flows from the supply to motor (both ν and i are positive and so are va and ia).
However, during π to π + α, some of the motor energy is fed back to the supply (v and i have opposite polarity and so are va and ia which means reversal of power flow). Observe that the fundamental of the current drawn from the mains lags the voltage by angle Φ1 = α.
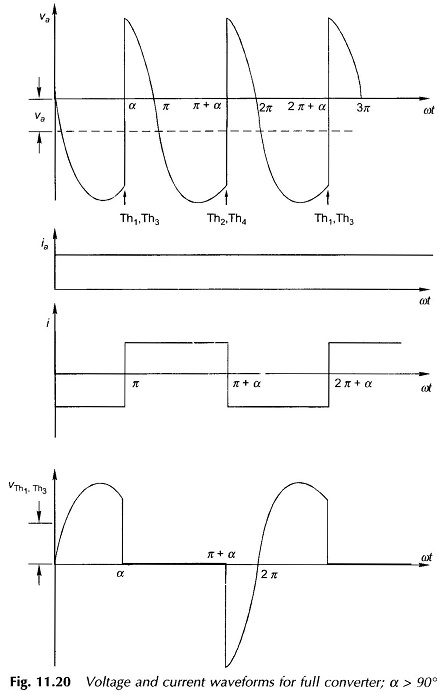
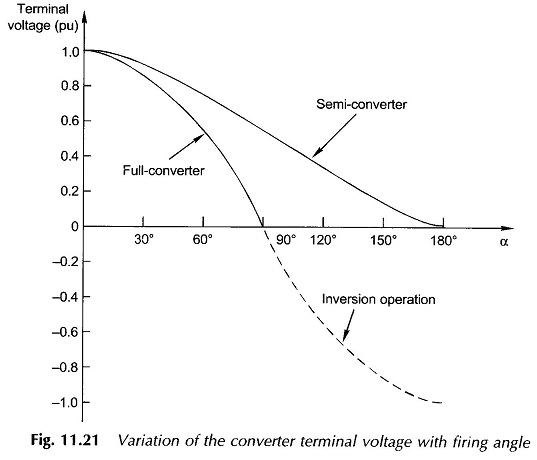
The voltage and current waveforms for α > 90° are shown in Fig. 11.20. The average motor terminal voltage is now negative. If the motor terminals are reversed, it will act as a generator feeding power back to the ac supply. This is the inversion operation of the converter and is used in regenerative braking of the motor. One point needs to be noted here. During the conduction period of either Th1Th3 or Th2Th4 as the supply voltage becomes negative, the armature current begins to reduce, causing the inductance polarity to reverse so that the conducting thyristors continue to be forward-biased.
The voltage and current waveforms for the case of discontinuous armature current can be found as in the case of the semi-converter. (see Fig. 11.20).
Torque-Speed Characteristics:
It will be assumed here that the armature current is continuous. For a semiconverter with free-wheeling diode action, the armature circuit equations are
For a full-converter, the armature circuit equation is
Let ν = √2 V sin ωt . The average motor terminal voltages are: With a semi-converter,
With a full-converter,
Figure 11.21 gives the variation of the motor terminal voltage as a function of the firing angle for both the semi-converter and full-converter. In the case of the full-converter inversion operation occurs for 90° < α < 180°.
The motor equations for average values are
and
Substituting for Ia from Eq. (11.8) and Va from Eqs (11.5) or (11.6) in Eq. (11.9), the speed-torque characteristics are given as follows:
With a semi-converter,
With a full-converter
The first term in Eqs. (11.10) and (11.11) represents the theoretical no-load speed while the second term represents speed drop caused by armature resistance. The theoretical no-load speed can be varied by the firing angle α.
In the case of discontinuous current, the average voltage at motor terminals depends upon the angle β (extinction angle) which itself is dependent on the average motor speed n, average motor current Ia and firing angle α. The analytical treatment of this case is beyond the scope of this book.
Dual-Converter:
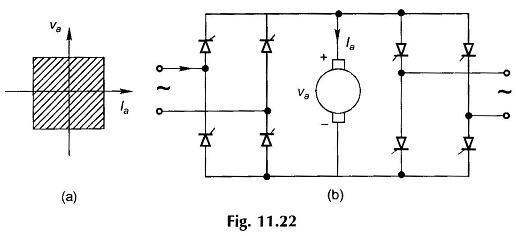
The dual-converter can operate in all the four quadrants as shown in Fig. 11.22(a). Its circuit is shown in Fig. 11.22(b). It is indeed two full-converters converting to dc in either direction. The dual converter provides virtually instantaneous reversal of voltage at dc terminals.
Control of DC Series Motor:
Semi-converters and full-converters are also employed for control of a dc series motor. The total circuit inductance is high because of the series field, as a consequence of which the armature current is mostly continuous. The governing motor equations differ as the flux/pole is now proportional to the armature current. The treatment otherwise is similar to that of a separately excited DC Motor Control and will not be pursued here for want of space.