CoTree and Tree in Circuit Analysis:

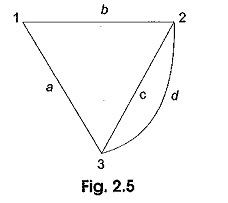
CoTree and Tree in Circuit Analysis – A tree is a connected subgraph of a network which consists of all the nodes of the original graph but no closed paths. The graph of a network may have a number of trees. The number of nodes in a graph is equal to the number nodes in the tree. The number of branches in a tree is less than the number of branches in a graph. A graph is a tree if there is a unique path between any pair of nodes. Consider a graph with four branches and three nodes as shown in Fig. 2.5.

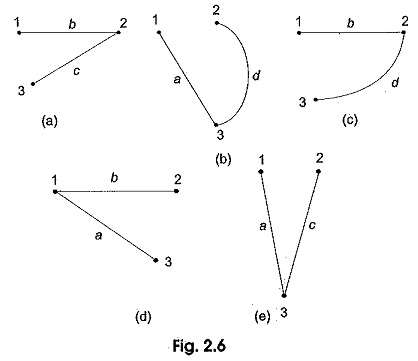
Five open-ended graphs based on Fig. 2.5 are represented by Figs 2.6 (a) to (e). Since each of these open-ended graphs satisfies all the requirements of a tree, each graph in Fig. 2.6 is a free corresponding to Fig. 2.5.

In Fig. 2.6, there is no closed path or loop; the number of nodes n = 3 is the same for the graph and its tree, where as the number of branches in the tree is only two. In general, if a tree contains n nodes, then it has (n-1) branches.

In forming a tree for a given graph, certain branches are removed or opened. The branches thus opened are called links or link branches. The links for Fig. 2.6 (a) for example area and d and for 2.6 (b) are b and c. The set of all links of a given tree is called the cotree of the graph. Obviously, the branches a, d are a co-tree for Fig. 2.6 (a) and b, c are the cotree. Similarly, for the tree in Fig. 2.6 (b), the branches b, c are the cotree. Thus the link branches and the tree branches combine to form the graph of the entire network.