Components of Load Torques:

Components of Load Torques T_l can be further divided into following components:

(i) Friction torque T_F :

Friction will be present at the motor shaft and also in various parts of the load. T_F is equivalent value of various friction torques referred to the motor shaft.

(ii) Windage torque, T_w :

When a motor runs, wind generates a torque opposing the motion. This is known as windage torque.

(iii) Torque required to do the useful mechanical work, T_L:

Nature of this Components of Load Torques depends on particular application. It may be constant and independent of speed; it may be some function of speed; it may depend on the position or path followed by load; it may be time invariant or time-variant; it may vary cyclically and its nature may also change with the load’s mode of operation.

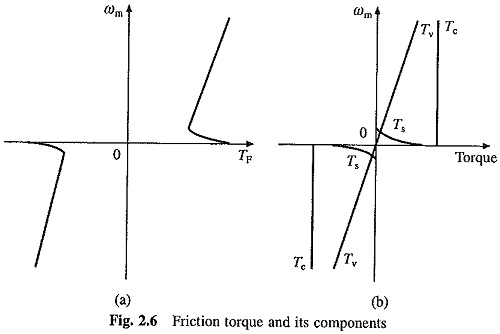
Variation of friction torque with speed is shown in Fig. 2.6(a). Its value at standstill is much higher than its value slightly above zero speed. Friction at zero speed is called stiction or static friction. In order for drive to start, the motor torque should at least exceed stiction. Friction torque can be resolved into three components (see Fig. 2.6(b)). Component T_v which varies linearly with speed is called viscous friction and is given by:

where B is the viscous friction coefficient.

Another component T_c, which is independent of speed, is known as Coulomb friction. Third component T_s accounts for additional torque present at standstill. Since T_s is present only at standstill it is not taken into account in the dynamic analysis.

Windage torque T_w, which is proportional to speed squared, is given by

where C is a constant.

From the above discussion, for finite speeds,

In many applications (T_c + Cω²_m) is very small compared to Bω_m and negligible compared to T_L. In order to simplify the analysis, term (T_c + Cω²_m) is approximately accounted by updating the value of viscous friction coefficient, B. With this approximation, from Eq. (2.2)

If there is a torsional elasticity in shaft coupling the load to the motor, an additional Components of Load Torques, known as Coupling Torque, will be present. Coupling torque (T_e) is given by

where θ_e is the torsion angle of coupling (radians) and K_e the rotational stiffness of the shaft (N­m/rad).

In most applications, shaft can be assumed to be perfectly stiff and coupling torque T_e can be neglected. Its presence in appreciable magnitude has adverse effects on motor. There is potential energy associated with coupling torque and kinetic energy with the dynamic torque. Exchange of energy between these two energy storage’s tends to produce oscillations which are damped by viscous friction torque Bω_m. When B is small, oscillations occur producing noise. Further, shaft may also break when the drive is started.