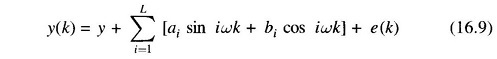Estimation Techniques of Periodic Components:
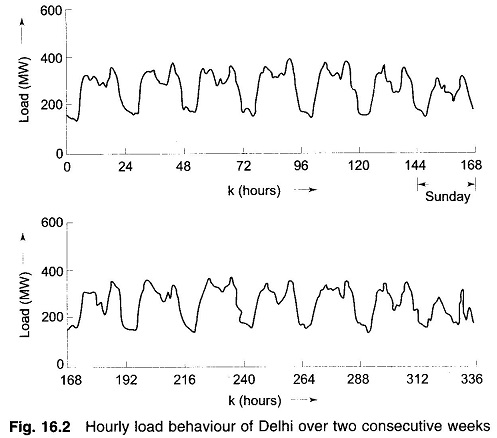
Estimation Techniques of Periodic Components – The deterministic part of the load may contain some periodic components in addition to the average and the polynomial terms. Consider for example the curve shown in Fig. 16.2 which gives the variation of the active power supplied by a power utility over a period of two weeks.
It is observed that the daily load variations are repetitive from day to day except for some random fluctuations. It is also seen that the curve for Sundays differ significantly from those of the week days in view that Sundays are holidays. It turns out that the curve for the entire weekly period starting from, say, the mid night of one Sunday till the mid night of the next Sunday behaves as a distinctly periodic waveform with superposed random variations.
If it is assumed that the load data are being sampled at an hourly interval, then there are a total of 168 load data in one period so that the load pattern may be expressed in terms of a Fourier series with the fundamental frequency ω being equal to 2π/168 rads. A suitable model for the load y(k) is then given by
where L represents the total number of harmonics present and ai and bi are the amplitudes of respectively the sinusoidal and the cosinusoidal components. Only dominant harmonics need to be included in the model.
Once the harmonic load model is identified, it is simple to make a prediction of the future load yd(k + j) using the relation