Standard Impulse Wave Shapes:

Transient overvoltages due to lighting and switching surges cause steep build-up of voltage on transmission lines and other electrical apparatus. Experimental investigations showed that these waves have a rise time of 0.5 to 10 μs and decay time to 50% of the peak value of the order of 30 to 200 μs. The Standard Impulse Wave Shapes are arbitrary, but mostly unidirectional. It is shown that lightning overvoltage wave can be represented as double exponential waves defined by the equation

where α and β are constants of microsecond values.

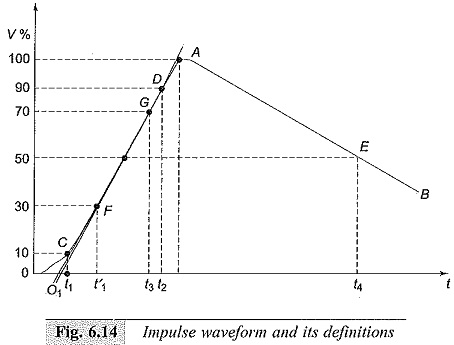
The above equation represents a unidirectional wave which usually has a rapid rise to the peak value and slowly falls to zero value. The general waveshapes is given in Fig. 6.14. Standard Impulse Wave Shapes are specified by defining their rise of front time, fall or tail time to 50% peak value, and the value of the peak voltage. Thus 1.2/50 μs, 1000 kV wave represents an impulse voltage wave with a front time of 1.2 μs, fall time to 50% peak value of 50 μs, and a peak value of 1000 kV.

When impulse waveshapes are recorded, the initial portion of the wave may not be clearly defined or sometimes may be missing. Moreover, due to disturbances it may contain superimposed oscillations in the rising portion. Hence, the front and tail times have to be redefined.

Referring to the waveshape in Fig. 6.14, the peak value A is fixed and referred to as 100% value. The points corresponding to 10% and 90% of the peak values are located in the front portion (points C and D). The line joining these points is extended to cut the time axis at O₁. O₁ is taken as the virtual origin. 1.25 times the interval between times t₁ and t₂ corresponding to points C and D (projections on the time axis) is defined as the front time, i.e. 1.25 (O₁t₂ – O₁t₁).

The point E is located on the wave tail corresponding to 50% of the peak value, and its projection on the time axis is t₄. O₁t₄ is defined as the fall or tail time. In case the point C is not clear or missing from the waveshape record, the point corresponding to 30% peak value F is taken and its projection t′₁ is located on time axis.

The wavefront time in that case will be defined as 1.67 (O₁t₃ – O₁t′₁). The tolerances that can be allowed in the front and tail times are respectively ± 30% and ± 20%. Indian standard specifications define 1.2/50 μs wave to be the standard lightning impulse. The tolerance allowed in the peak value is ± 3%.

Theoretical Representation of Impulse Waves:

The Standard Impulse Wave Shapes are generally represented by Eq. (6.15) given earlier. V₀ in the equation represents a factor that depends on the peak value. For impulse wave of 1.2/50 μs, α= – 0.0146,β = – 2.467, and V₀ = 1.04 when time t is expressed in microseconds, α and β control the front and tail times of the wave respectively.