Interaction of Circuit Breaker:
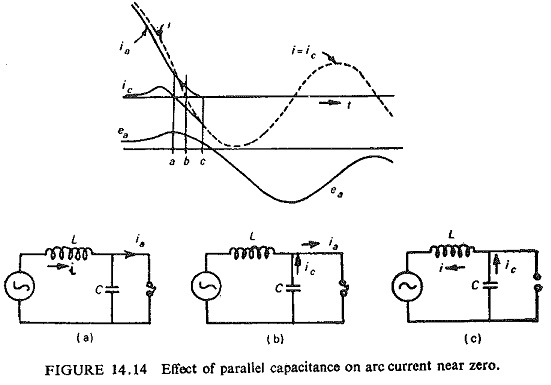
The circuit breaker performance can well be seen from the interaction between the breaker and the circuit. It is convenient to regard the short-circuit current i in the period around current zero as composed of two parts: the arc current ia and the transient current ic flowing in the capacitive part of the circuit which determines the restriking voltage. The voltage across the circuit breaker ea is related to ia by the dynamic characteristics of the arc and also to ic by the inherent transient response of the external circuit, while at any instant before or after zero i = ic + ia. Figure (14.14) shows in schematic form how the current across the capacitance C aids interruption by lowering the current immediately before zero.
If e is the supply voltage in the circuit then the equation of the circuit can be written as e = L di/dt + ea. Considering the events occurring from the time when ea begins to rise, this causes a diversion of current into the shunt capacitance C given by ic = C dea/dt. This current is positive and since ia = i – ic, it is obtained at the expense of the arc current which therefore starts to fall more rapidly than i. Now as the instant a is approached, the rate of fall of ia diminishes and at instant a, dea/dt = 0, ic=0, and ia = i (Fig. (14.14a)). Immediately after this the capacitance C starts discharging giving negative ic, whereas i and ia are still positive, so that the arc is supplied from both the source and the capacitance, obviously during this period ia is greater than i. At instant b when i reaches zero, Fig. (14.14b), the arc is supplied only by the capacitance ia = ic and i=0. After this instant the current i reverses, and the difference constitutes ia. In the negative direction i rises at a faster rate than ic until at instant c, i = ic and the arc is extinguished, i.e. ia= 0 (Fig. (14.14c)).
The interaction between arc and circuit can be calculated around current zero, if the time constant τ and rate of power dissipation of the arc, as well as the initial conditions of the interaction interval are known. These values can be measured and put into a mathematical arc model, which has to be combined with the differential equation of the circuit. The voltage required to maintain an arc at a given current may be much less when the current has been decreasing rapidly than in the static case.
The heat balance of the arc, and hence its temperature and conductivity, is determined by P = eaia (the electrical power input) and P0 (the rate of heat removal by the blast). If R is taken as the instantaneous value of the arc resistance and τ the thermal time constant, we obtain
For successful clearance R continues to increase after current zero. With the aid of computer it is possible to calculate the curves of current and voltage around current zero and to decide whether or not residual conductance and thermal reignition of the arc path occurs.