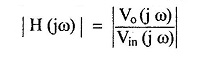Filters in Linear Integrated Circuits:
The Filters in Linear Integrated Circuits can be represented in the time domain and frequency domain as shown in Fig. 2.73 (a) and (b).
As the filter is frequency selective network, the output Vo(t) contains only some of the frequency components of Vin (t). It is convenient to analyze the filter by representing it in a frequency domain as shown in Fig. 2.73 (b). In the frequency domain, the filter is described by the transfer function,
where
- ω = 2πf and
- f is the operating frequency.
In the steady state, the transfer function can be represented in the polar form as,
where
- M = | H(jω) | = magnitude
- φ = ∠ H (jω) = phase angle
The magnitude is generally represented in dB as 20 log | H (jω) |. In the frequency response of various filters discussed above, the magnitude i.e. gain is plotted against the frequency. Thus, the magnitude of the transfer function is
called gain of the filter. The Filters in Linear Integrated Circuits are analyzed and designed considering the magnitude and the phase angle of the transfer function.
An important thing can be observed from the frequency responses discussed above is the behavior of the gain in the stop band for the various filters. The frequency response either decreases or increases or both in the stop band. The rate at which the gain of the filter changes in the stop band is dependent on the order of the filter.
If the filter is first order then gain increases at a rate 20 dB/decade in a stop band of high pass filter, the gain decreases at a rate 20 dB/decade in a stop band of low pass filter and so on. This indicates that there is a change of 20 dB in a gain per decade (10times) change in the frequency. Such a change in gain is called Gain Roll off. In case of a second order filters, the gain roll off is at the rate of 40 dB/decade and so on.
The various types of Filters in Linear Integrated Circuits used, in practice which approximately produce the ideal response are
- Butterworth filters
- Chebyshev Filters
- Cauer Filters