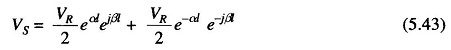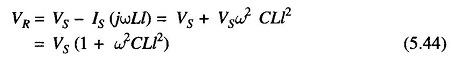Ferranti Effect in Transmission Line:

The effect of the line capacitance is to cause the no-load receiving-end voltage to be more than the sending-end voltage. The effect becomes more pronounced as the line length increases. This phenomenon is known as the Ferranti Effect in Transmission Line. A general explanation of this effect is advanced below:

Substituting x = l and I_R = 0 (no-load) in Eq. (5.21), we have

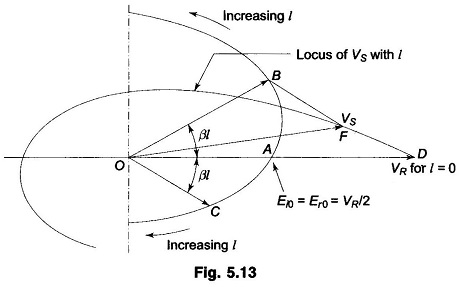
The above equation shows that at l = 0, the incident (E_i0) and reflected (E_r0) voltage waves are both equal to V_R/2. With reference to Fig. 5.13, as l increases, the incident voltage wave increases exponentially in magnitude (V_R/2 e^αl) and turns through a positive angle βl (represented by phasor OB); while the reflected voltage wave decreases in magnitude exponentially (V_R/2 e^–αl) and turns through a negative angle βl (represented by phasor OC).

It is apparent from the geometry of this figure that the resultant phasor voltage V_S (OF) is such that |V_R| > |V_S|.

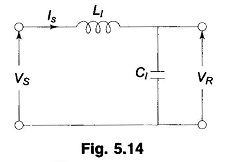
A simple explanation of the Ferranti Effect in Transmission Line on an approximate basis can be advanced by lumping the inductance and capacitance parameters of the line. As shown in Fig. 5.14 the capacitance is lumped at the receiving-end of the line.

Here

Since C is small compared to L, ωLl can be neglected in comparison to 1/ωCl.

Thus

Now

Magnitude of voltage rise = |V_S|ω² CLl²

where ν = 1/√LC is the velocity of propagation of the electromagnetic wave along the line, which is nearly equal to the velocity of light.