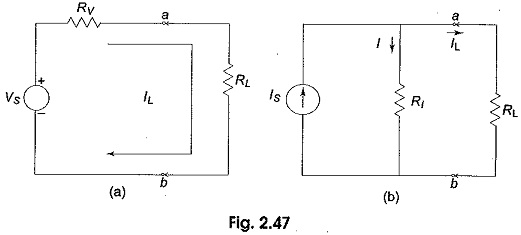
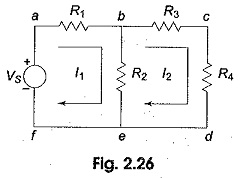
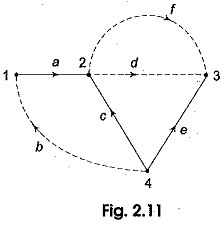
Source Transformation Technique: Source Transformation Technique - In solving networks to find solutions one may have to deal with energy sources. It has already been discussed before that basically, energy Source Transformation are either voltage…
Supernode Analysis: Suppose any of the branches in the network has a voltage source, then it is slightly difficult to apply nodal analysis. One way to overcome this difficulty is to apply the Supernode Analysis.…
Nodal Analysis Examples: Nodal Analysis Examples - we discussed simple circuits containing only two nodes, including the reference node. In general, in a N node circuit, one of the nodes is chosen as reference or…
Super Mesh Circuit Analysis: Suppose any of the branches in the network has a current source, then it is slightly difficult to apply mesh analysis straight forward because first we should assume an unknown voltage…
Mesh Analysis Equation: Mesh Analysis Equation and nodal analysis are two basic important techniques used in finding solutions for a network. The suitability of either mesh or nodal analysis to a particular problem depends mainly on…
Cut Set Matrix and Tree Branch Voltages: A Cut Set Matrix is a minimal set of branches of a connected graph such that the removal of these branches causes the graph to be cut into…
Tie Set Matrix(Link Currents): Tie Set Matrix - For a given tree of a graph, addition of each link between any two nodes forms a loop called the fundamental loop. In a loop there exists…
Incidence Matrix (A): The incidence of elements to nodes in a connected graph is shown by the element node incidence matrix (A). Arrows indicated in the branches of a graph result in an oriented or…
Twigs and Links: Twigs and Links - The branches of a tree are called its 'twigs'. For a given graph, the complementary set of branches of the tree is called the co-tree of the graph.…
CoTree and Tree in Circuit Analysis: CoTree and Tree in Circuit Analysis - A tree is a connected subgraph of a network which consists of all the nodes of the original graph but no closed…
