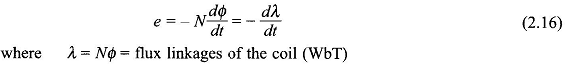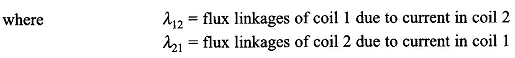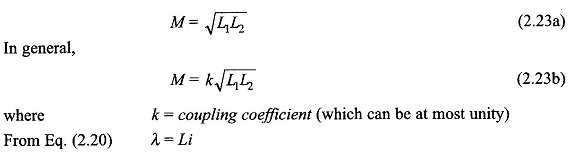Magnetically Induced Emf and Force:
Magnetically Induced Emf and Force – Faraday’s law of induction, which is the integral form of the fourth Maxwell’s equation, is given as![]()
The integrated form of Eq.(2.15) for a coil of N turns is
The positive direction of current in the coil is that direction which establishes positive flux and flux linkages. The negative sign in Eq. (2.16) means that the Magnetically Induced Emf and Force owing to an increase in λ is in opposite direction to that of positive current. If this fact is separately remembered (it is known as Lenz’s law), Eq. (2.16) may be written as
with the sign of the emf determined by Lenz’s law.
Change in flux linkages of a coil may occur in three ways:
- The coil remains stationary with respect to flux, but the flux through it changes with time. The emf induced is known as statically Magnetically Induced Emf and Force.
- Flux density distribution remains constant and stationary but the coil moves relative to it. The emf induced is known as dynamically induced (or motional) emf.
- Both changes (i) and (ii) may occur simultaneously, i.e. the coil moves through time-varying flux. Both statically and dynamically induced emfs are then present in the coil.
The dynamically Magnetically Induced Emf and Force (case (ii) above) in a conductor of length / placed at 90° to a magnetic field of flux density B and cutting across it at speed ν is given by
where θ is the angle between the direction of flux density and conductor velocity, and l the conductor along which the flux density is assumed uniform. In electric machines θ = 90°, so that
This is known as the flux-cutting rule and the direction of emf is given by ν x B or by the well-known Fleming’s right-hand rule.
Inductance:
Equation (2.17) may be written as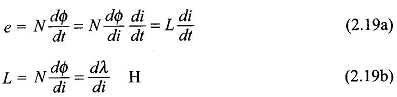
is the self-inductance of the circuit. For a magnetic circuit having a linear B-H relationship (constant permeability of material) or with a dominating air-gap, the inductance L is a constant, independent of current and depends only on the geometry of circuit elements and permeability of the medium. In this case Eq. (2.19) can also be expressed as
The inductance can be written in terms of field quantities as
Thus self-inductance is proportional to N2. The inductance concept is easily extendable to the mutual inductance of two coils sharing a common magnetic circuit. Thus,
For a bilateral magnetic circuit,
It can also be shown that for tight coupling, i.e. all the flux linking both the coils (no leakage)
In static magnetic configuration, L is fixed independent of time so that the induced emf is given by Eq. (2.19a). In rotating devices both L and i vary with time giving the induced emf
Force:
Force of electromagnetic origin is given by the Lorentz force equation
where I is the current flowing in the differential conductor of length dl. Integrating over the conductor length along which B is assumed uniform, the total force is obtained as
where θ is the angle between the direction of conductor and the magnetic field and af, is unit vector in the direction defined by the cross product. For θ = 90° which is used in most machine configurations, Eq. (2.26a) reduces to
The direction of force being given by Il x B or by the well-known Fleming’s left hand rule. It immediately follows from Eq. (2.26b) that B can be imagined to have unit of N/Am.