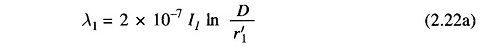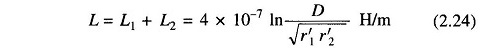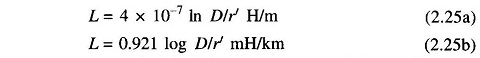Inductance of Single Phase Two Wire Line:
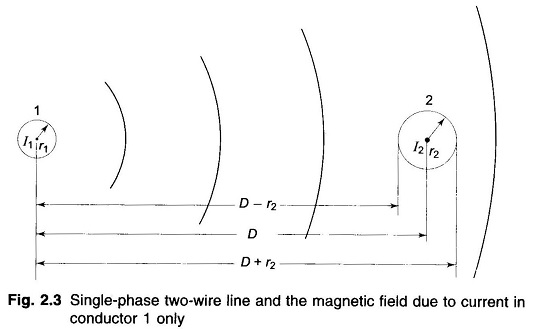
Inductance of Single Phase Two Wire Line – Consider a simple Two Wire Line composed of solid round conductors carrying currents I1 and I2 as shown in Fig. 2.3. In a Single Phase Line,
It is important to note that the effect of earth’s presence on magnetic field geometry is insignificant. This is so because the relative permeability of earth is about the same as that of air and its electrical conductivity is relatively small.
To start with, let us consider the flux linkages of the circuit caused by current in conductor 1 only.
We make three observations in regard to these flux linkages of Inductance of Single Phase Two Wire Line:
- External flux from r1 to (D – r2) links all the current I1 in conductor 1.
- External flux from (D – r2) to (D + r2) links a current whose magnitude progressively reduces from I1 to zero along this distance, because of the effect of negative current flowing in conductor 2.
- Flux beyond (D + r2) links a net current of zero.
For calculating the total inductance due to current in conductor 1, a simplifying assumption will now be made. If D is much greater than r1 and r2 (which is normally the case for overhead lines), it can be assumed that the flux from (D – r2) to the centre of conductor 2 links all the current I1 and the flux from the centre of conductor 2 to (D + r2) links zero current.
Based on the above assumption, the flux linkages of the circuit caused by current in conductor 1 as per Eq. (2.21a) are
The inductance of the conductor due to current in conductor 1 only is then
Similarly, the inductance of the circuit due to current in conductor 2 is
Using the superposition theorem, the flux linkages and likewise the inductances of the circuit caused by current in each conductor considered separately may be added to obtain the total circuit inductance. Therefore, for the complete circuit
Transmission lines are infinitely long compared to D in practical situations and therefore the end effects in the above derivation have been neglected.