Control of AC Motors Torque Control:

From the foregoing discussion for Control of AC Motors Torque Control it is clear that the motors used for textile applications must have

• high starting torque
• torque control providing uniform acceleration so that the breakage of the yarn is minimum and the quality of the product is improved. 

The production increases if the down time of the process and drive is reduced.

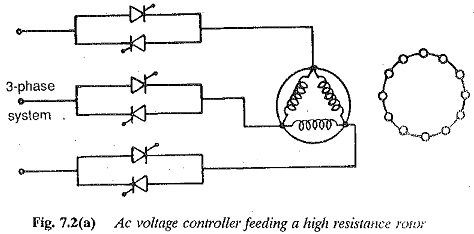
In conventional drive systems the Control of AC Motors Torque Control is achieved by variation of applied voltage to the squirrel cage motors. In slip ring induction motors torque control is possible by means of rotor resistance control. The variation of applied voltage is realised by series connected reactors on the stator side. The torque control in stepless. The accelerating energy keeps the constant tension in the yarn. The resistances, even though they have advantages, are not employed as their heating may cause fire hazards.

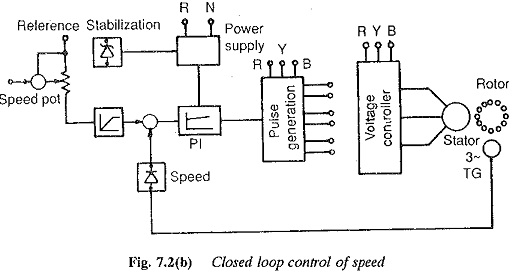
With the development of thyristor power converters the applied voltage variation to an induction motor for torque control is accomplished by means of ac voltage controller in the supply circuit. Closed loop control can be employed (Fig. 7.2).

This method of using reduced voltage for Control of AC Motors Torque Control, however, has disadvantages of poor power factor at reduced voltages.

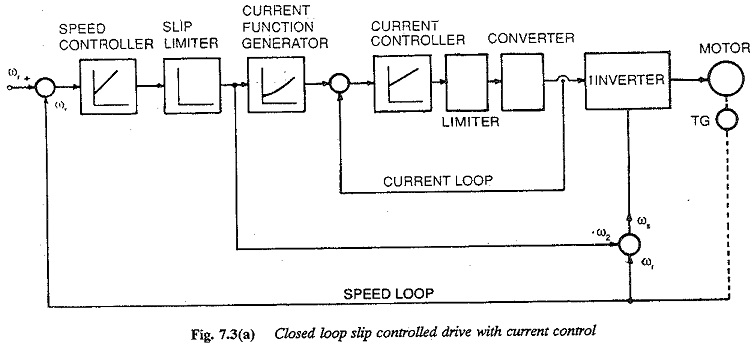
The torque control as well as speed control is obtained using induction motors fed from variable frequency inverters. The inverter is controlled such that the motor operates with constant flux, to achieve the best possible torque capability of the motor. Both voltage source and current source inverters can be employed. Slip controlled drives assure uniform starting torque. For smooth low speed operation cycloconverters are preferred (Fig. 7.3).

With slip ring rotors, chopper controlled resistance may be used for Control of AC Motors Torque Control.

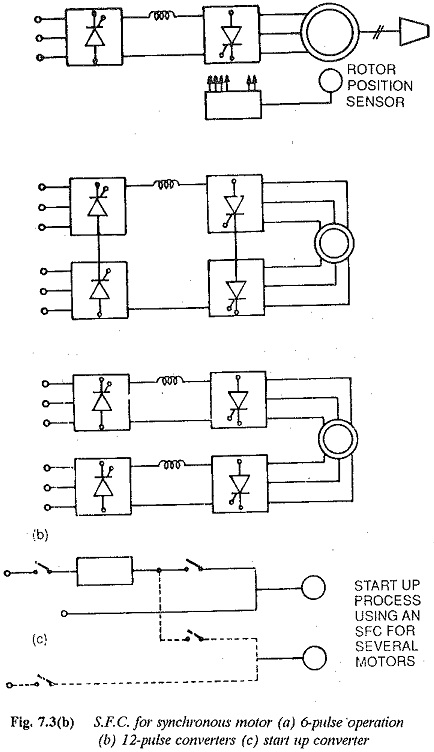
Converter fed synchronous motors are also becoming very popular. They have the advantages that the converter can employ machine commutation, in which case the inverter configuration is simple. A self control of the motor converter imparts dc motor characteristics, where the problems of hunting and stability are not there. For low speeds cycloconverters are preferred. Voltage source and current source link inverters can also be used for control of synchronous motors.

For other processes, such as bleaching, drying, printing, finishing, etc., in textile mills, the normal motors are used. When very low speeds are required, gearing may be employed. Ward Leonard dc drive, ac commutator motors are employed. The thyristor control may be used where efficient, smooth speed control over a wide range is required.

Special design of textile mill motors are required owing to the location of the motor, running conditions and also the torque requirements while starting. In textile mills the motors are located in places where there is a lot of dust. The cotton fluff may be deposited on the motor, which affects natural cooling of the motor. Consequently the temperature rise of the motor is more, which may heat the cotton fluff leading to fire. To prevent this situation and also prevent the dust and fluff entering the interior of the motor the motors must be totally enclosed and fan cooled (to keep the surface clean). Also the motors employed for the job of bleaching, etc., must have proper enclosure to prevent any possible damage. If a group drive is employed the motor may be located outside the room. The motors must be designed to withstand thermal variations under the Worst conditions.