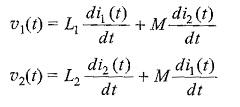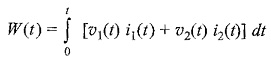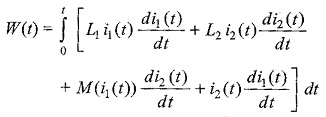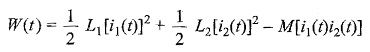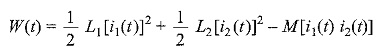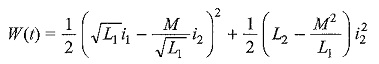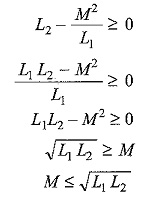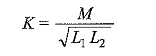Coefficient of Coupling:
The amount of coupling between the inductively coupled coils is expressed in terms of the coefficient of coupling, which is defined as
where
- M = mutual inductance between the coils
- L1 = self inductance of the first coil, and
- L2 = self inductance of the second coil
Coefficient of coupling is always less than unity, and has a maximum value of 1 (or 100%). This case, for which K = 1, is called perfect coupling, when the entire flux of one coil links the other. The greater the coefficient of coupling between the two coils, the greater the mutual inductance between them, and vice-versa. It can be expressed as the fraction of the magnetic flux produced by the current in one coil that links the other coil.
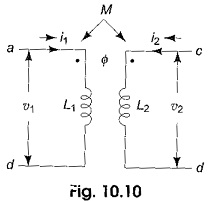
For a pair of mutually coupled circuits shown in Fig. 10.10, let us assume initially that i1, i2 are zero at t = 0.
Initial energy in the coupled circuit at t = 0 is also zero. The net energy input to the system shown in Fig. 10.10 at time t is given by
Substituting the values of υ1(t) and υ2(t) in the above equation yields
From which we get
If one current enters a dot-marked terminal while the other leaves a dot marked terminal, the above equation becomes
According to the definition of passivity, the net electrical energy input to the system is non-negative. W(t) represents the energy stored within a passive network, it cannot be negative.
The statement can be proved in the following way. If i1 and i2 are both positive or negative, W(t) is positive. The other condition where the energy equation could be negative is
The above equation can be rearranged as
The first term in the parenthesis of the right side of the above equation is positive for all values of i1 and i2, and, thus, the last term cannot be negative; hence
Obviously the maximum value of the mutual inductance is √L1L2. Thus, we define the coefficient of coupling for the coupled circuit as
The coefficient, K, is a non negative number and is independent of the reference directions of the currents in the coils. If the two coils are a great distance apart in space, the mutual inductance is very small, and K is also very small. For iron-core coupled circuits, the value of K may be as high as 0.99, for air-core coupled circuits, K varies between 0.4 to 0.8.