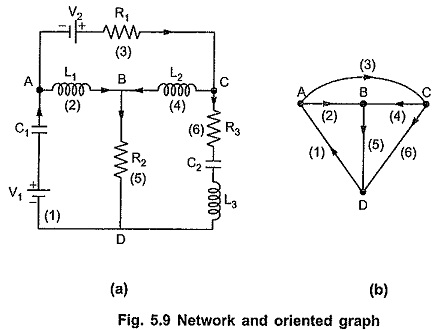
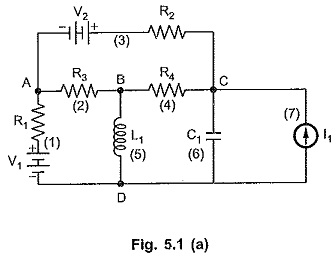
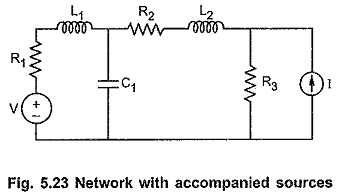
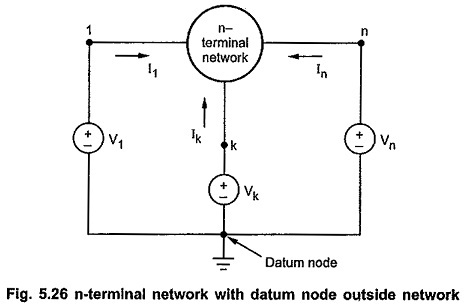
Graph Theory Network Analysis: To analyse a network means to find current through any branch or voltage across any branch. We can analyse given network using Graph Theory Network Analysis by relating branch currents and…
Cut Set Matrix in Network Analysis: A connected graph can be separated into two parts by removing certain branches of the graph. This is equivalent to cutting a graph into two parts hence it is…
Loop Matrix or Circuit Matrix: For a given directed graph, it is always possible to state which branches are involved in the formation of loops or closed circuits or meshes. For a given oriented graph,…
Define Incidence Matrix: Define Incidence Matrix consists of two parts, namely Complete Incidence Matrix Reduced Incidence Matrix Complete Incidence Matrix (Aa): Define Incidence Matrix is nothing but a mathematical model to represent the given network…
Network Topology: Basically network analysis is nothing but finding unknown branch currents or voltages across various branches. We can find these unknown parameters by using different network simplification techniques. These network simplifications involves basic Kirchhoff's…
V Shift and I Shift Method: V Shift and I Shift Method - A voltage source with a passive branch in series with it is called an accompanied voltage source. Similarly a current source with…
Network Equilibrium Equation in Matrix Form: In earlier section we have studied how to obtain equilibrium equations for a network which are based on loop analysis and node analysis. We can represent the same Network…
Indefinite Admittance Matrix: Consider Indefinite Admittance Matrix of a linear network with n terminals as shown in the Fig. 5.26. Let us consider a zero potential reference node or datum node arbitrarily outside the n-terminal…
