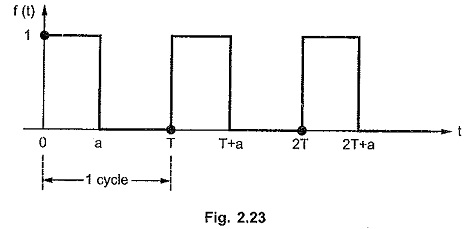
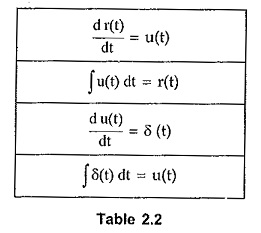
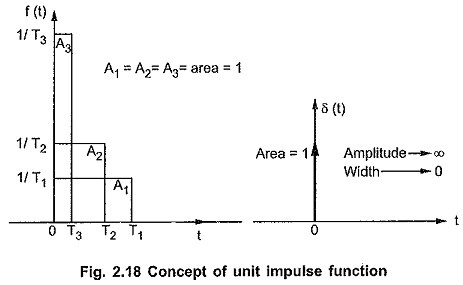
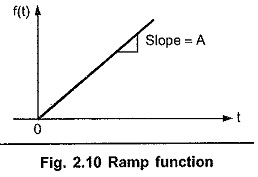
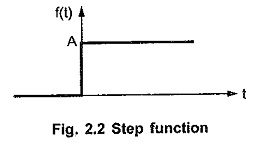
Convolution Integral in Network Analysis
Convolution Integral in Network Analysis: The Convolution Integral in Network Analysis in Laplace transform states that where f1 (t) * f2 (t) = Convolution of f1 (t) and f2 (t) From the definition of system function, Taking inverse Laplace,…