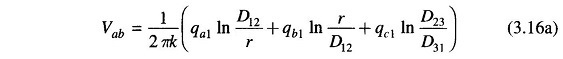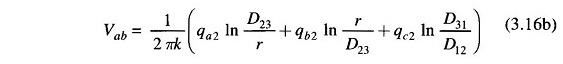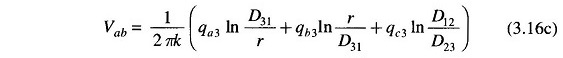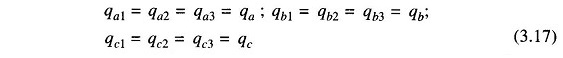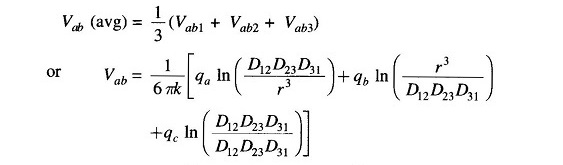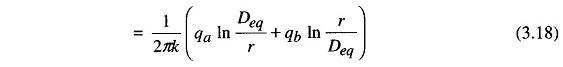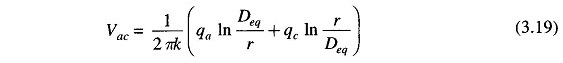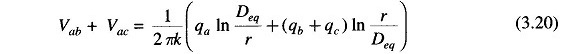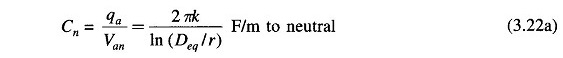Capacitance of Three Phase Line with Unsymmetrical Spacing:
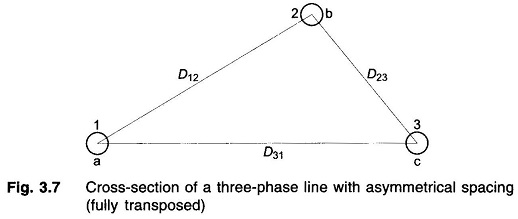
Figure 3.7 shows the three identical conductors of radius r of a Capacitance of Three Phase Line with Unsymmetrical Spacing. It is assumed that the line is fully transposed. As the conductors are rotated cyclically in the three sections of the transposition cycle, correspondingly three expressions can be written for Vab. These expressions are:
For the first section of the transposition cycle
For the second section of the transposition cycle
For the third section of the transposition cycle
If the voltage drop along the line is neglected, Vab is the same in each transposition cycle. On similar lines three such equations can be written for Vbc = Vab ∠ –120°. Three more equations can be written equating to zero the summation of all line charges in each section of the transposition cycle. From these nine (independent) equations, it is possible to determine the nine unknown charges. The rigorous solution though possible is too involved.
With the usual spacing of conductors sufficient accuracy is obtained by assuming
This assumption of equal charge/unit length of a line in the three sections of the transposition cycle requires, on the other hand, three different values of Vab designated as Vab1, Vab2 and Vab3 in the three sections. The solution can be considerably simplified by taking Vab as the average of these three voltages, i.e.
where
Similarly,
Adding Eqs. (3.18) and (3.19), we get
As per Eq. (3.12) for balanced three-phase voltages
and also
Use of these relationships in Eq. (3.20) leads to
The capacitance of line to neutral of the transposed line is then given by
For air medium (kr = 1)
It is obvious that for equilateral spacing Deq = D, the above (approximate) formula gives the exact result presented earlier.
The line charging current for a Capacitance of Three Phase Line with Unsymmetrical Spacing in phasor form is