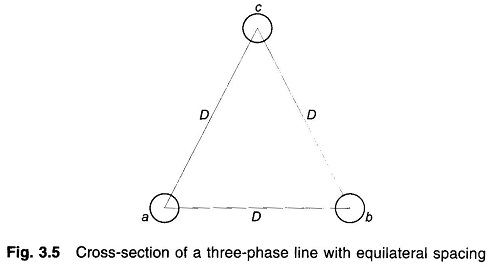
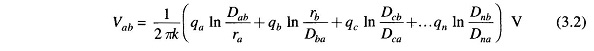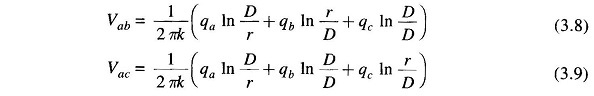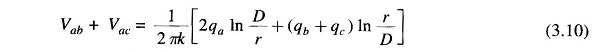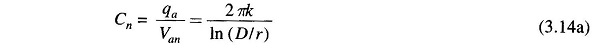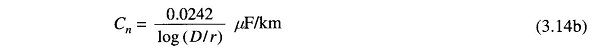Capacitance of Three Phase Transmission Line with Equilateral Spacing:
Figure 3.5 shows a Capacitance of Three Phase Transmission Line with Equilateral Spacing composed of three identical conductors of radius r placed in equilateral configuration.
Using Eq. (3.2) we can write the expressions for Vab and Vac as
Adding Eqs. (3.8) and (3 9), we get
Since there are no other charges in the vicinity, the sum of charges on the three conductors is zero. Thus qb + qc = – qa, which when substituted in Eq. (3.10) yields
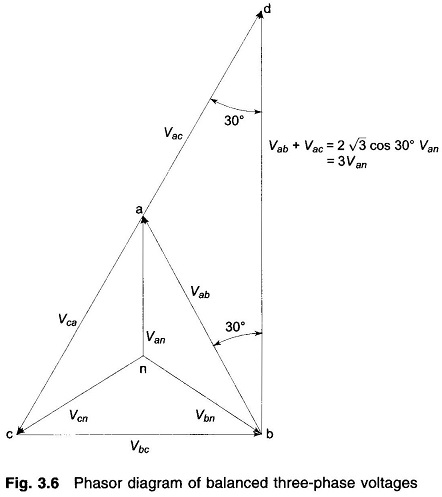
With balanced three-phase voltages applied to the line, it follows from the phasor diagram of Fig. 3.6 that
Substituting for (Vab + Vac) from Eq. (3.12) in Eq. (3.11), we get
The capacitance of line to neutral immediately follows as
For air medium (kr = 1),
The line charging current of phase a is