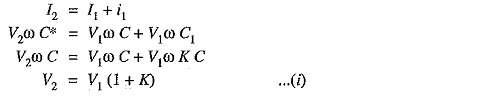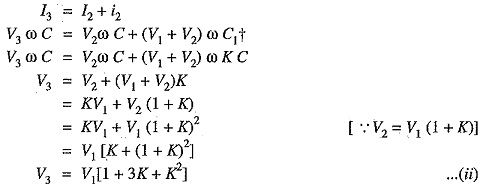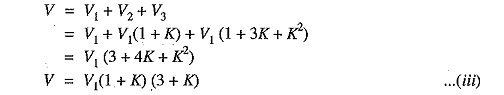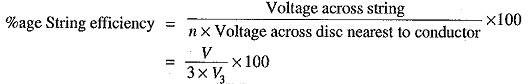String Efficiency of Insulator:

As stated above, the voltage applied across the string of suspension insulators is not uniformly distributed across various units or discs. The disc nearest to the conductor has much higher potential than the other discs. This unequal potential distribution is undesirable and is usually expressed in terms of String Efficiency of Insulator.

The ratio of voltage across the whole string to the product of number of discs and the voltage across the disc nearest to the conductor is known as string efficiency i.e.,

String Efficiency of Insulator is an important consideration since it decides the potential distribution along the string. The greater the string efficiency, the more uniform is the voltage distribution. Thus 100% string efficiency is an ideal case for which the voltage across each disc will be exactly the same. Although it is impossible to achieve 100% string efficiency, yet efforts should be made to improve it as close to this value as possible.

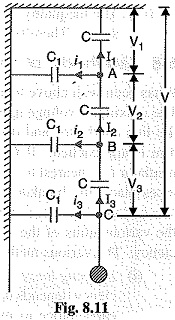
Mathematical expression: Fig. 8.11 shows the equivalent circuit for a 3-disc string. Let us suppose that self capacitance of each disc is C. Let us further assume that shunt capacitance C₁ is some fraction K of self capacitance i.e., C₁ = KC. Starting from the cross-arm or tower, the voltage across each unit is V₁, V₂ and V₃ respectively as shown.

Applying Kirchhoff’s current law to node A, we get,

Applying Kirchhoff’s current law to node B, we get,

Voltage between conductor and earth (i.e., tower) is

From expressions (i), (ii) and (iii), we get,

Voltage across top unit,

Voltage across second unit from top, V₂ = V₁ (1 + K)

Voltage across third unit from top, V₃ = V₁ (1 + 3K + K²)

The following points may be noted from h above mathematical analysis :

• If K = 0.2 (Say), then from exp. (iv), we get, V₂ = 1.2 V₁ and V₃ = 1.64 V₁. This clearly shows that disc nearest to the conductor has maximum voltage across it; the voltage across other discs decreasing progressively as the cross-arm in approached.
• The greater the value of K (= C₁/C), the more non-uniform is the potential across the discs and lesser is the String Efficiency of Insulator.
• The inequality in voltage distribution increases with the increase of number of discs in the Therefore, shorter string has more efficiency than the larger one

Methods of Improving String Efficiency

It has been seen above that potential distribution in a string of suspension insulators is not uniform. The maximum voltage appears across the insulator nearest to the line conductor and decreases progressively as the cross-arm is approached. If the insulation of the highest stressed insulator (i.e. nearest to conductor) breaks down or flash over takes place, the breakdown of other units will take place in succession. This necessitates to equalize the potential across the various units of the string i.e. to improve the string efficiency.

The various methods for this purpose are :

1.By using longer cross-arms. The value of String Efficiency of Insulator depends upon the value of K i.e., ratio of shunt capacitance to mutual capacitance. The lesser the value of K, the greater is the String Efficiency of Insulator and more uniform is the voltage distribution. The value of K can be decreased by reducing the shunt capacitance. In order to reduce shunt capacitance, the distance of conductor from tower must be increased i.e., longer cross-arms should be used. However, limitations of cost and strength of tower do not allow the use of very long cross-arms. In practice, K =0.1 is the limit that can be achieved by this method.

2.By grading the insulators. In this method, insulators of different dimensions are so chosen that each has a different capacitance. The insulators are capacitance graded i.e. they are assembled in the string in such a way that the top unit has the minimum capacitance, increasing progressively as the bottom unit (i.e., nearest to conductor) is reached. Since voltage is inversely proportional to capacitance, this method tends to equalize the potential distribution across the units in the string. This method has the disadvantage that a large number of different-sized insulators are required. However, good results can be obtained by using standard insulators for most of the string and larger units for that near to the line conductor.

3.By using a guard ring. The potential across each unit in a string can be equalized by using a guard ring which is metal ring electrically connected to the conductor and surrounding the bottom insulator as shown in the Fig. 8.13. The guard ring introduces capacitance between metal fittings and the line conductor. The guard ring is contoured in such a way that shunt capacitance currents i₁,i₂ etc. are equal to metal fitting line capacitance currents i′₁,i′₂ etc. The result is that same charging current I flows through each unit of string. Consequently, there will be uniform potential distribution across the units.