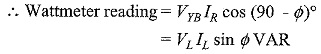Reactive Power with Wattmeter:
We have already seen earlier that the difference between higher reading wattmeter and lower reading wattmeter yields VLIL sin Φ. So, the total reactive power = √3 VLIL sin Φ. Reactive Power with Wattmeter in a balanced three-phase load can also be calculated by using a single wattmeter.
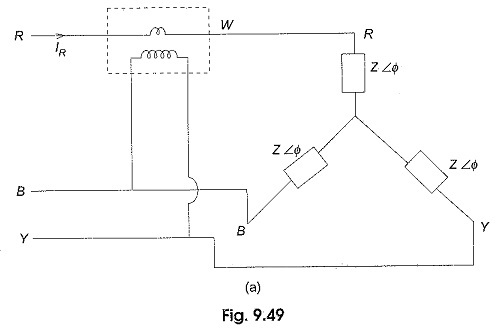
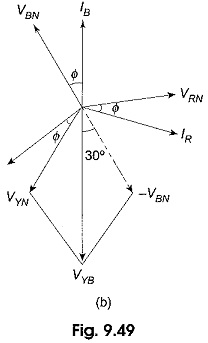
As shown in Fig. 9.49(a), the current coil of the wattmeters is connected in any one line (R in this case), and the pressure coil across the other two lines (between Y and B in this case). Assuming phase sequence RYB and an inductive load of angle Φ, the phasor diagram for the circuit in Fig. 9.49(a) is shown in Fig. 9.49(b).
From Fig. 9.49(a), if is clear that the wattmeter power is proportional to the product of current through its current coil, IR, voltage across its pressure coil, VYB, and cosine of the angle between VYB and IR.
or
From the vector diagram the angle between VYB and IR is (90 – Φ)°
If the above expression is multiplied by √3, we get the total Reactive Power with Wattmeter in the load.