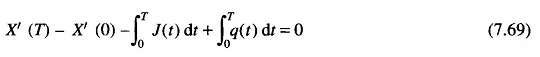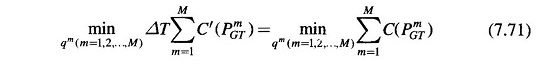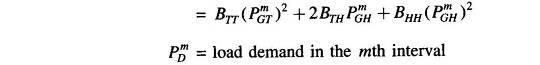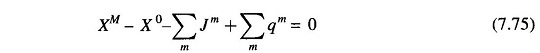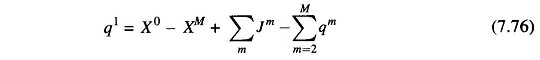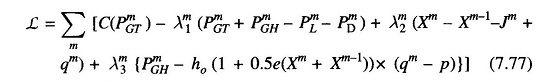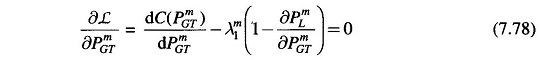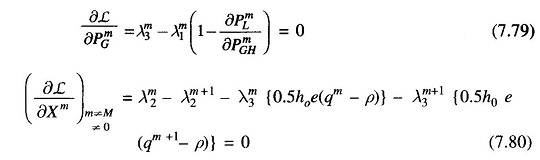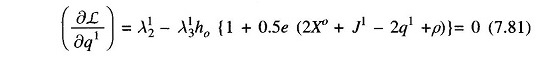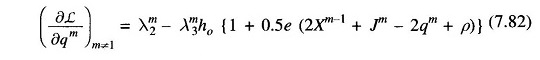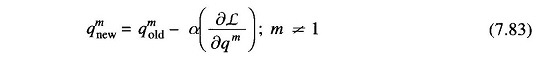Optimal Scheduling of Hydrothermal Processes:

The earlier sections have dealt with the problem of optimal scheduling of a power system with thermal plants only. Optimal operating policy in this case can be completely determined at any instant without reference to operation at other times. This, indeed, is the static optimization problem. Operation of a system having both hydro and thermal plants is, however, far more complex as hydro plants have negligible operating cost, but are required to operate under constraints of water available for hydro generation in a given period of time. The problem thus belongs to the realm of dynamic optimization. The problem of minimizing the operating cost of a Hydrothermal Processes can be viewed as one of minimizing the fuel cost of thermal plants under the constraint of water availability (storage and inflow) for hydro generation over a given period of operation.

Theory of Hydrothermal Processes:

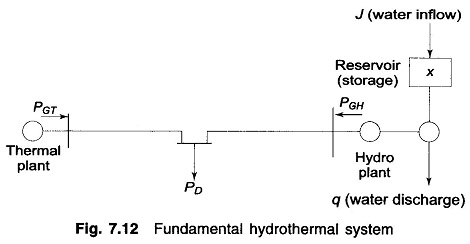
For the sake of simplicity and understanding, the problem formulation and solution technique are illustrated through a simplified Hydrothermal Processes of Fig. 7.12. This Hydrothermal System consists of one hydro and one thermal plant supplying power to a centralized load and is referred to as a Fundamental Hydrothermal System. Optimization will be carried out with real power generation as control variable, with transmission loss accounted for by the loss formula of Eq. (7.26).

Mathematical Formulation:

For a certain period of operation T (one year, one month or one day, depending upon the requirement), it is assumed that (i) storage of hydro reservoir at the beginning and the end of the period are specified, and (ii) water inflow to reservoir (after accounting for irrigation use) and load demand on the system are known as functions of time with complete certainty (deterministic case). The problem is to determine q(t), the water discharge (rate) so as to minimize the cost of thermal generation.

under the following constraints:

(i) Meeting the load demand

This is called the power balance equation.

(ii) Water availability

where J(t) is the water inflow (rate), X′(t) water storage, and X′(0), X′(T) are specified water storages at the beginning and at the end of the optimization interval.

(iii) The hydro generation P_GH(t) is a function of hydro discharge and water storage (or head), i.e. 

The problem can be handled conveniently by discretization. The optimization interval T is subdivided into M subintervals each of time length ΔT. Over each subinterval it is assumed that all the variables remain fixed in value. The problem is now posed as

under the following constraints:

(i) Power balance equation

Where

• P^m_GT = thermal generation in the mth interval
• P^m_GH = hydro generation in the mth interval
• P^m_L = transmission loss in the mth interval

(ii) Water continuity equation

where

• X′^m = water storage at the end of the mth interval
• J^m = water inflow (rate) in the mth interval
• q^m = water discharge (rate) in the mth interval

The above equation can be written as

where X^m = X^/m/ΔT = storage in discharge units.

In Eqs. (7.73), X^° and X^M are the specified storage’s at the beginning and end of the optimization interval.

(iii) Hydro generation in any subinterval can be expressed as

where

• h_o = 9.81 x 10^-3h′_o
• h_o = basic water  head ( head corresponding to dead storage)
• e = water head correction factor to account for head variation with storage
• ρ = non-effective discharge (water discharge needed to run hydro generator at no load).

In the above problem formulation, it is convenient to choose water discharges in all subintervals except one as independent variables, while hydro genera­tions, thermal generations and water storages in all subintervals are treated as dependent variables. The fact, that water discharge in one of the subintervals is a dependent variable, is shown below:

Adding Eq. (7.73) for m = 1, 2, …, M leads to the following equation, known as water availability equation

Because of this equation, only (M – 1) qs can be specified independently and the remaining one can then be determined from this equation and is, therefore, a dependent variable. For convenience, q¹ is chosen as a dependent variable, for which we can write

Solution Technique:

The problem is solved here using non-linear programming technique in conjunction with the first order gradient method. The Lagrangian ζ is formulated by augmenting the cost function of Eq. (7.71) with equality constraints of Eqs. (7.72)— (7.74) through Lagrange multipliers (dual variables) λ^m₁, λ^m₂ and λ^m₃. Thus,

The dual variables are obtained by equating to zero the partial derivatives of the Lagrangian with respect to the dependent variables yielding the following equations

and using Eq. (7.73) in Eq. (7.77), we get

The dual variables for any subinterval may be obtained as follows:

• Obtain λ^m₁ from Eq. (7.78).
• Obtain λ^m₃ from Eq. (7.79).
• Obtain λ¹₂ from Eq. (7.81) and other values of λ^m₂(m ≠ 1) from Eq. (7.80).

The gradient vector is given by the partial derivatives of the Lagrangian with respect to the independent variables. Thus

For optimality the gradient vector should be zero if there are no inequality constraints on the control variables.

Algorithm:

1. Assume an initial set of independent variables q^m (m≠1) for all subintervals except the first.
2. Obtain the values of dependent variables X^m, P^m_GH, P^m_GT, q¹ using Eqs.(7.73), (7.74), (7.72) and (7.76).
3. Obtain the dual variables λ^m₁, λ^m₃, λ^m₂ (m ≠ 1) and λ¹₂ using Eqs. (7.78), (7.79), (7.80) and (7.81).
4. Obtain the gradient vector using Eq. (7.82) and check if all its elements are equal to zero within a specified accuracy. If so, optimum is reached. If not, go to step 5.
5. Obtain new values of control variables using the first order gradient method, i.e.

where α is a positive scalar. Repeat from step 2.

In the solution technique presented above, if some of the control variables (water discharges) cross the upper or lower bounds, these are made equal to their respective bounded values.

Advantages and Disadvantages:

The Hydrothermal Processes method outlined above is quite general and can be directly extended to a system having multi-hydro and multi-thermal plants. The method, however, has the disadvantage of large memory requirement, since the independent variables, dependent variables and gradients need to be stored simultaneously. A modified technique known as decomposition overcomes this difficulty. In this technique optimization is carried out over each subinterval and the complete cycle of iteration is repeated, if the water availability equation does not check at the end of the cycle.