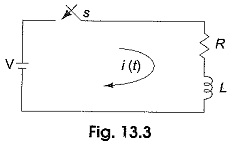
Application of Laplace Transform
Application of Laplace Transform: Application of Laplace Transform methods are used to find out transient currents in circuits containing energy storage elements. To find these currents, first the differential equations are formed by applying Kirchhoff's…