Quarter Wavelength Transmission Line:
Sections of transmission lines that are exactly a Quarter Wavelength Transmission Line or Half Wavelength Transmission Line long have important impedance-transforming properties, and are often used for this purpose at radio frequencies.
Impedance inversion by Quarter Wavelength lines:
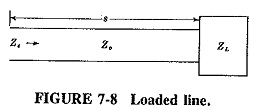
Consider Figure 7-8, which shows a load of impedance ZL connected to a piece of transmission line of length s and having Z0 as its characteristic impedance. When the length s is exactly a quarter-wavelength line (or an odd number of quarter-wavelengths) and the line is lossless, then the impedance Zs, seen when looking toward the load, is given by
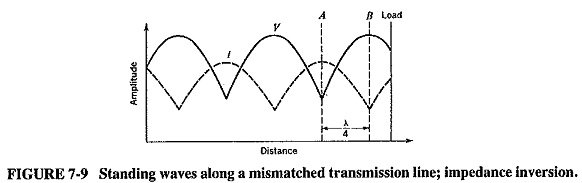
This relationship is sometimes called reflective impedance; i.e., the Quarter Wavelength Transmission Line reflects the opposite of its load impedance. Equation (7-10) represents a very important and fundamental relation, which is somewhat too complex to derive here, but whose truth may be indicated as follows. Unless a load is resistive and equal to the characteristic impedance of the line to which it is connected, standing waves of voltage and current are set up along the line, with a node (and antinode) repetition rate of λ/2. This has already been shown and is indicated again in Figure 7-9. Note that here the voltage and current minima are not zero; the load is not a short circuit, and therefore the standing-wave ratio is not infinite. Note also that the current nodes are separated from the voltage nodes by a distance of λ/4, as before.
It is obvious that at the point A (voltage node, current antinode) the line impedance is low, and at the point B (voltage antinode, current node) it is the reverse, i.e., high. In order to change the impedance at A, it would be necessary to change the SWR on the line. If the SWR were increased, the voltage minimum at A would be lower, and so would be the impedance at A. The size of the voltage maximum at B would be increased, and so would the impedance at B. Thus an increase in ZB is accompanied by a decrease in ZA (if A and B are λ/4 apart). This amounts to saying that the impedance at A is inversely proportional to the impedance at B. Equation (7-10) states this relation mathematically and also supplies the proportionality constant; this happens to be the square of the characteristic impedance of the transmission line. The relation holds just as well when the two points are not voltage nodes and antinodes, and a glance at Figure 7-9 shows that it also applies when the distance separating the points is three, five, seven and so on, quarter-wavelengths.
Another interesting property of the Quarter Wavelength Transmission Line is seen if, in Equation (7-10), the impedance are normalized with respect to Z0. Dividing both sides by Z0, we have
Hence Z0/ZL = 1/zL.
Substituting these results into Equation (8-11) gives
where yL is the normalized admittance of the load.
Equation (7-12) is a very important relation. It states that if a Quarter Wavelength Transmission Line is connected to an impedance, then the normalized input impedance of this line is equal to the normalized load admittance. Both must be normalized with respect to the line. Note that there is no contradiction here, since all normalized quantities are dimensionless. Note also that this relation is quite independent of the characteristic impedance of the line, a property that is very useful in practice.
Quarter-wave transformer and impedance matching:
In nearly all transmission-line applications, it is required that the load be matched to the line. This involves the tuning out of the unwanted load reactance (if any) and the transformation of the resulting impedance to the value required. Ordinary RF transformers may be used up to the middle of the VHF range. Their performance is not good enough at frequencies much higher than this, owing to excessive leakage inductance and stray capacitance. The Quarter Wavelength Transmission Line provides unique opportunities for impedance transformation up to the highest frequencies and is compatible with transmission lines.
Equation (7-10) shows that the impedance at the input of a Quarter Wavelength Transmission Line depends on two quantities: these are the load impedance (which is fixed for any load at a constant frequency) and the characteristic impedance of the interconnecting transmission line. If this Z0 can be varied, the impedance seen at the input to the λ/4 transformer will be varied accordingly, and the load may thus be matched to the characteristic impedance of the main line. This is similar to varying the turns ratio of a transformer to obtain a required value of input impedance for any given value of load impedance.
It must be understood that a quarter-wave transformer has a length of λ/4 at only one frequency. It is thus highly frequency-dependent, and is in this respect similar to a high-Q tuned circuit. As a matter of fact, the difference between the transmission line transformer and an ordinary tuned transformer is purely one of construction, the practical behavior is identical. This property of the quarter-wave transformer makes it useful as a filter, to prevent undesirable frequencies from reaching the load, often an antenna. If broadband impedance matching is required, the transformer must be constructed of high-resistance wire to lower its Q, thereby increasing bandwidth.
It should be mentioned that the procedure .becomes somewhat more involved if the load is complex, rather than purely resistive as so far considered. The quarter-wave transformer can still be used, but it must now be connected at some precalculated distance from the load. It is generally connected at the nearest resistive point to the load, whose position may be found with the aid of a transmission-line calculator, such as a Smith chart.
Half-wavelength line:
As was mentioned previously, the reflected impedance is an important characteristic of the matching process; the half-wavelength line reflects its load impedance directly. A half-wave transformer has the property that the input impedance must be equal to the impedance of the load placed at the far end of the half-wave line. This property is independent of the characteristic impedance of this line, but once, again it is frequency-dependent.
The advantages of this property are many. For instance, it is very often not practicable to measure the impedance of a load directly. This being the case, the impedance may be measured along a transmission line connected to the load, at a distance which is a half-wavelength (or a whole number of half-wavelengths) from the load. Again, it is sometimes necessary to short-circuit a transmission line at a point that is not physically accessible. The same results will be obtained if the short circuit is placed a half-wavelength (etc.) away from the load. Yet again, if a short-circuited half-wave transmission line is connected across the main line, the main line will be short-circuited at that point, but only at the frequency at which the shunt line is a half-wavelength. That frequency will not pass this point, but others will, especially if they are farther and farther away from the initial frequency. The short-circuited shunt half-wave line has thus become a band-stop filter. Finally, if the frequency of a signal is known, a short-circuited transmission line may be connected to the generator of this frequency, and a half-wavelength along this line may be measured very accurately. From the knowledge of frequency and wavelength, the velocity of the wave along the line can be calculated. We may determine the velocity factor, and therefore the dielectric constant of the insulation.